0 40331 40339 40345 40349 40355 40357 40361 40367 40369 40375 40381 40385 40387 40391 40397 40399 40405 40409 40411 40415 40417 40421 40423 40425 40426 40427 40429 40430 40431 40433 40435 40439 40441 40445 40447 40451 40457 40459 40465 40469 40471 40475 40481 40487 40489 40495 40499 40501 40507 40511 40517 40525 447348
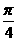 个单位,沿y轴向下平移
个单位,沿y轴向下平移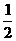 个单位,得到g(x)的图象,已知g(x)的图象关于(
个单位,得到g(x)的图象,已知g(x)的图象关于(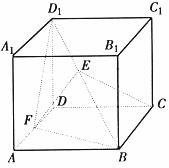 正四棱柱ABCD-A1B1C1D1中,已知AB=2,E,F分别是D1B,AD的中点,cos
正四棱柱ABCD-A1B1C1D1中,已知AB=2,E,F分别是D1B,AD的中点,cos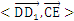 =
=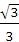 .
.
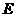 的方程为
的方程为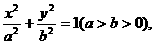 双曲线
双曲线 的两条渐近线为
的两条渐近线为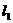 和
和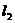 ,过椭圆
,过椭圆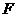 作直线
作直线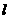 ,使得
,使得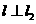 于点
于点 ,又
,又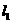 交于点
交于点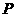 ,
,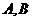 (如图).
(如图).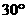 ,双曲线的焦距为8时,求椭圆的方程;
,双曲线的焦距为8时,求椭圆的方程;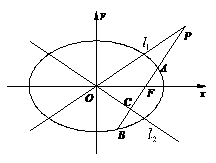 (2)设
(2)设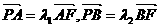 ,证明:
,证明: 为常数.
为常数.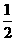 ,乙、丙面试合格的概率都是
,乙、丙面试合格的概率都是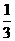 ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求: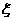 的分布列和数学期望.
的分布列和数学期望.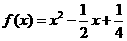 ,
,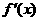 为函数
为函数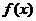 的导函数.
的导函数.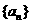 满足:
满足: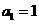 ,
,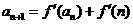 (
(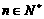 ) 求数列
) 求数列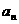 ;
;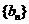 满足:
满足: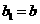 ,
,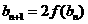 (
(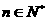 ).
).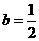 时,数列
时,数列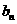 ;若不是,请说明理由;
;若不是,请说明理由;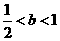 时,求证:
时,求证: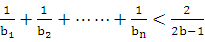
 的六个面着色,要求相邻两个面颜色不相同,则不同的着色方法种数有
的六个面着色,要求相邻两个面颜色不相同,则不同的着色方法种数有
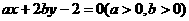 始终平分圆的周
始终平分圆的周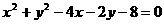 长,则
长,则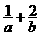 的最小值为
的最小值为
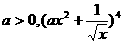 的展开式中,
的展开式中, 的系数为
的系数为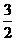 ,
,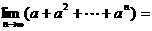 。
。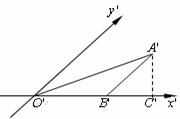 如图是利用斜二测画法画出的
如图是利用斜二测画法画出的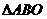 的直观图,已知
的直观图,已知 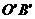 =4,且
=4,且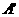 作
作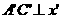 轴,则
轴,则 的长为 。
的长为 。