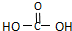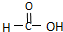摘要:16 向量a=.b=.其中0<ω<l.且a∥b.将f(x)的图象沿x轴向左平移个单位.沿y轴向下平移个单位.得到g的图象关于(.0)对称 (1)求ω的值, 在[0.4π]上的单调递增区间. 17 正四棱柱ABCD-A1B1C1D1中.已知AB=2.E.F分别是D1B.AD的中点.cos=. (1)建立适当的坐标系.求出E点的坐标, (2)证明:EF是异面直线D1B与AD的公垂线, (3)求二面角D1-BF-C的余弦值. 18 某机床厂今年年初用98万元购进一台数控机床.并立即投入生产使用.计划第一年维修.保养费用12万元.从第二年开始.每年所需维修.保养费用比上一年增加4万元.该机床使用后.每年的总收入为50万元.设使用x年后数控机床的盈利总额为y万元. (1)写出y与x之间的函数关系式, (2)从第几年开始.该机床开始盈利 (3)使用若干年后.对机床的处理方案有两种:(Ⅰ)当年平均盈利额达到最大值时.以30万元价格处理该机床,(Ⅱ)当盈利额达到最大值时.以12万元价格处理该机床. 请你研究一下哪种方案处理较为合理?请说明理由. 19 已知椭圆的方程为双曲线的两条渐近线为和.过椭圆的右焦点作直线.使得于点.又与交于点.与椭圆的两个交点从上到下依次为. (1)当直线的倾斜角为.双曲线的焦距为8时.求椭圆的方程, (2)设.证明:为常数. 20 甲.乙.丙三人参加了一家公司的招聘面试.面试合格者可正式签约.甲表示只要面 试合格就签约,乙.丙则约定:如果两人面试都合格就一同签约.否则两人都不签约.设甲面试合格的概率为.乙.丙面试合格的概率都是.且面试是否合格互不影响.求: (1)至少有1人面试合格的概率; (2)签约人数的分布列和数学期望. 21 已知函数.为函数的导函数. (1)若数列满足:.() 求数列的通项, (2)若数列满足:.(). ①当时.数列是否为等差数列?若是.请求出数列的通项,若不是.请说明理由, ②当时.求证:
网址:http://m.1010jiajiao.com/timu3_id_404287[举报]
(2009?泰州模拟)已知A是一种有机溶剂,F 是一种黄色晶体,N带有磁性,B、F、L、O、P是中学化学常见单质,J的相对分子质量比D大16,A和B反应前后气体体积(常温常压)保持不变,在试管中灼烧固体I,试管底部无固体残留,反应①②③均是化工生产中的重要反应.
实验装置图

(1)A的结构式
(2)写出反应①的化学方程式
(3)高温下反应⑤⑥互为可逆反应,写出反应⑥的化学方程式
该反应的平衡常数表达式K=
.
(4)请设计一个实验方案,完成反应④,并绘出实验装置图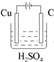
 .
.
查看习题详情和答案>>
实验装置图

(1)A的结构式
S=C=S
S=C=S
.(2)写出反应①的化学方程式
NaCl+CO2+H2O+NH3=NaHCO3↓+NH4Cl
NaCl+CO2+H2O+NH3=NaHCO3↓+NH4Cl
.(3)高温下反应⑤⑥互为可逆反应,写出反应⑥的化学方程式
3Fe+4H2O(g) Fe3O4+4H2
Fe3O4+4H2
 Fe3O4+4H2
Fe3O4+4H23Fe+4H2O(g) Fe3O4+4H2
Fe3O4+4H2
, Fe3O4+4H2
Fe3O4+4H2该反应的平衡常数表达式K=
| c4(H2) |
| c4(H2O) |
| c4(H2) |
| c4(H2O) |
(4)请设计一个实验方案,完成反应④,并绘出实验装置图


物质 R2CO3 的饱和溶液 V mL,密度为 ρ g?cm-3,c(R+)=P mol?L-1,溶质的质量分数为 a%,溶质的式量为 M,溶质的溶解度为sg.则下列表达式正确的是( )
A、a=
| ||
B、s=
| ||
C、P=
| ||
D、V×ρ×a%=
|
某种ABS工程树脂,由丙烯腈(CH2=CHCN,符号A).1,3-丁二烯(CH2=CH-CH=CH2,符号B)和苯乙烯(C6H5-CH=CH2,符号S)按一定配比共聚而得.
(1)A.B和S三种单体中,碳氢比(C:H)值最小的单体是
(2)经元素分析可知该ABS样品的组成为CaHbNc(a.b.c为正整数),则原料中A和B的物质的量之比是
查看习题详情和答案>>
(1)A.B和S三种单体中,碳氢比(C:H)值最小的单体是
1,3-丁二烯
1,3-丁二烯
.(2)经元素分析可知该ABS样品的组成为CaHbNc(a.b.c为正整数),则原料中A和B的物质的量之比是
c:
| b-a |
| 2 |
c:
(用a.b.c表示).| b-a |
| 2 |
已知A是一种有机溶剂,F是一种黄色粉末,N有磁性;B、F、L、O、P是中学化学常见单质;J的相对分子质量比D大16;A和B反应前后气体体积(常温常压)保持不变;在试管中灼烧固体I,试管底部无固体残留;反应①②③均是化工生产中的重要反应.

(1)C的电子式为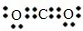
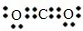 .
.
(2)A与B反应的化学方程式为
(3)反应①的化学方程式为
(4)反应④的离子方程式为
(5)高温下由反应⑤生成6molP时共转移
查看习题详情和答案>>

(1)C的电子式为
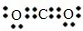
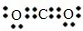
(2)A与B反应的化学方程式为
CS2+3O2
CO2+2SO2
| ||
CS2+3O2
CO2+2SO2
.
| ||
(3)反应①的化学方程式为
NaCl+NH3+CO2+H2O=NaHCO3↓+NH4Cl
NaCl+NH3+CO2+H2O=NaHCO3↓+NH4Cl
.(4)反应④的离子方程式为
Cu+2H+
Cu2++H2↑
| ||
Cu+2H+
Cu2++H2↑
.
| ||
(5)高温下由反应⑤生成6molP时共转移
16
16
mol电子.