0 139165 139173 139179 139183 139189 139191 139195 139201 139203 139209 139215 139219 139221 139225 139231 139233 139239 139243 139245 139249 139251 139255 139257 139259 139260 139261 139263 139264 139265 139267 139269 139273 139275 139279 139281 139285 139291 139293 139299 139303 139305 139309 139315 139321 139323 139329 139333 139335 139341 139345 139351 139359 447348
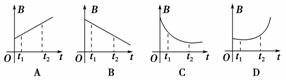
 答案:CD
答案:CD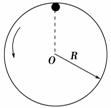 答案:B
答案:B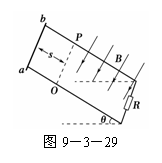 如图9-3-29所示,有一足够长的光滑平行金属导轨,
如图9-3-29所示,有一足够长的光滑平行金属导轨,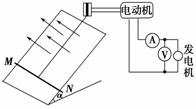
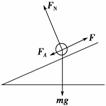
 (2010·江苏单科,13)如图9-3-27所示,两足够长的光滑
(2010·江苏单科,13)如图9-3-27所示,两足够长的光滑 如图9-3-26所示,在一水平桌面上有竖直向上的匀强磁
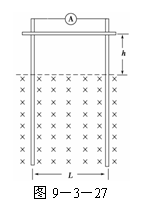
如图9-3-26所示,在一水平桌面上有竖直向上的匀强磁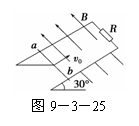 一质量为m、电阻为r的金属杆ab,以一定的初速度v0从一
一质量为m、电阻为r的金属杆ab,以一定的初速度v0从一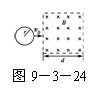 如图9-3-24所示,在光滑的水平面上,一质量为m,半径为r,电
如图9-3-24所示,在光滑的水平面上,一质量为m,半径为r,电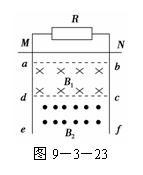 如图9-3-23所示,光滑的“
如图9-3-23所示,光滑的“ ”形金属导体框竖直放置,质
”形金属导体框竖直放置,质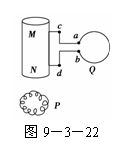 如图9-3-22所示,Q是单匝金属线圈,
如图9-3-22所示,Q是单匝金属线圈,