0 139168 139176 139182 139186 139192 139194 139198 139204 139206 139212 139218 139222 139224 139228 139234 139236 139242 139246 139248 139252 139254 139258 139260 139262 139263 139264 139266 139267 139268 139270 139272 139276 139278 139282 139284 139288 139294 139296 139302 139306 139308 139312 139318 139324 139326 139332 139336 139338 139344 139348 139354 139362 447348
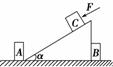 如图2-2-29所示,一倾角为α的斜面体置于固定在光滑水平地面
如图2-2-29所示,一倾角为α的斜面体置于固定在光滑水平地面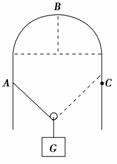 在上海世博会最佳实践区,江苏城市案例馆中穹形门窗充满了浓郁
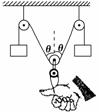
在上海世博会最佳实践区,江苏城市案例馆中穹形门窗充满了浓郁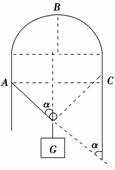 解析:由于轻绳中各处的张力相等,若两悬挂点之间的水平距离为
解析:由于轻绳中各处的张力相等,若两悬挂点之间的水平距离为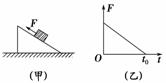
 (2011·青岛检测)如图2-2-26所示,质量为m的两木块a和b叠放
(2011·青岛检测)如图2-2-26所示,质量为m的两木块a和b叠放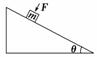 斜面的压力F=kt(k为比例常量,t为时间)作用在物体上.从t=0开
斜面的压力F=kt(k为比例常量,t为时间)作用在物体上.从t=0开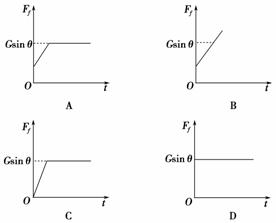
 答案:B
答案:B 答案:C
答案:C
 如图9-2-27所示,两根平行金属导轨固定在同一水平面
如图9-2-27所示,两根平行金属导轨固定在同一水平面