0 138921 138929 138935 138939 138945 138947 138951 138957 138959 138965 138971 138975 138977 138981 138987 138989 138995 138999 139001 139005 139007 139011 139013 139015 139016 139017 139019 139020 139021 139023 139025 139029 139031 139035 139037 139041 139047 139049 139055 139059 139061 139065 139071 139077 139079 139085 139089 139091 139097 139101 139107 139115 447348
 ,其他各部分电阻均不计.开始时,磁感应强度B0=0.50T
,其他各部分电阻均不计.开始时,磁感应强度B0=0.50T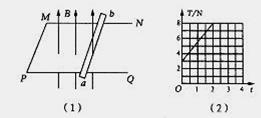 (2)若从某时刻t=0开始,调动磁感应强度的大小使其以
(2)若从某时刻t=0开始,调动磁感应强度的大小使其以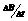 =0.20 T/s的变化率均匀增加.求经过多长时间ab棒开始滑动?此时通过ab棒的电流大小和方向如何?(ab棒与导轨间的最大静摩擦力和滑动摩擦力相等) ,
=0.20 T/s的变化率均匀增加.求经过多长时间ab棒开始滑动?此时通过ab棒的电流大小和方向如何?(ab棒与导轨间的最大静摩擦力和滑动摩擦力相等) ,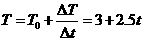
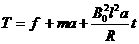
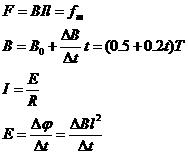

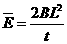 ...............................1分
...............................1分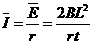 ...........................................1分
...........................................1分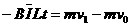 .............................1分
.............................1分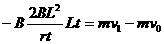
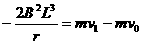
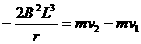
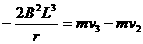
 ................................1分
................................1分 .......................................1分
.......................................1分 ............................................1分
............................................1分 ...........................................1分
...........................................1分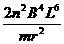 ................................................1分
................................................1分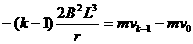 ......................2分
......................2分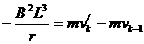 .....................1分
.....................1分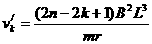 .........................1分
.........................1分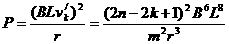 ...............................2分
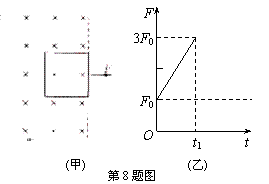
...............................2分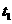 时刻穿出磁场.已知外力F随时间变化的图像如图(乙)所示,且线框的质量m、电阻R、图(乙)中的
时刻穿出磁场.已知外力F随时间变化的图像如图(乙)所示,且线框的质量m、电阻R、图(乙)中的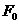 、
、
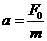 ①
①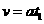 ②
②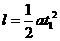 ③
③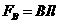 ④
④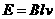 ⑤
⑤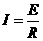 ⑥
⑥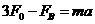 ⑦
⑦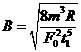 ⑧
⑧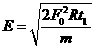 ⑨
⑨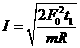 ⑩
⑩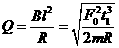 ⑾
⑾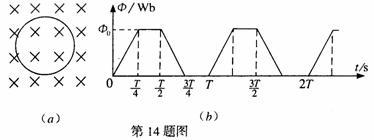 都是已知量,求
都是已知量,求 的时间内,通过金属圆环某横截面的电荷量q.
的时间内,通过金属圆环某横截面的电荷量q.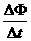 ①
①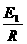 ②
②
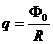 ④
④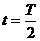 和在
和在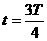 到t =T时间内,环中的感应电动势
到t =T时间内,环中的感应电动势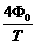 ⑥
⑥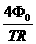 ⑦
⑦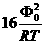 ⑨
⑨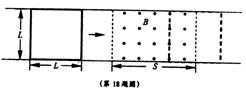
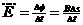 (1分)
(1分)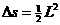 (1分)
(1分)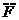 安=
安= 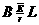 : (1分)
: (1分)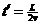 (1分)
(1分)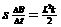 (2分)
(2分)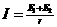 ('分)
('分)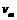 ,则有:
,则有: 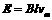 ①
①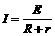 ②
②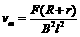 ④
④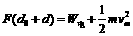 ⑤
⑤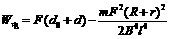 ⑥
⑥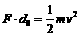 ⑦
⑦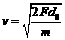 ⑧
⑧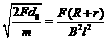 (或
(或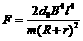 ),则棒做匀速直线运动;
),则棒做匀速直线运动;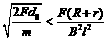 (或F>
(或F>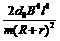 ),则棒先加速后匀速;
),则棒先加速后匀速;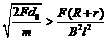 (或F<
(或F<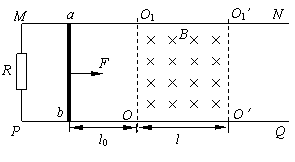
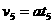
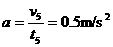 ……………………………⑥
……………………………⑥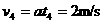 ……………………………⑦
……………………………⑦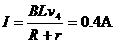 ……………………⑧
……………………⑧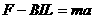
 ……………………⑨
……………………⑨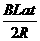 (4分)
(4分)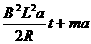 (4分)
(4分)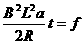 +T0
+T0
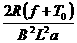 (4分)
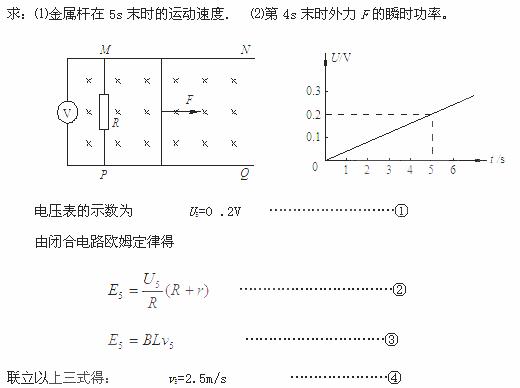
(4分)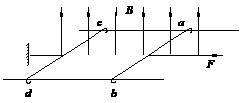 如图所示,在方向竖直向上的磁感应强度为B的匀强磁场中,有两条足够长的平行金属导轨,其电阻不计,间距为L,导轨平面与磁场方向垂直。ab、cd为两根垂直导轨放置的、电阻都为R、质量都为m的金属棒。棒cd用能承受最大拉力为T0的水平细线拉住,棒cd与导轨间的最大静摩擦力为f 。棒ab与导轨间的摩擦不计,在水平拉力F的作用下以加速度a由静止开始向右做匀加速直线运动,求:
如图所示,在方向竖直向上的磁感应强度为B的匀强磁场中,有两条足够长的平行金属导轨,其电阻不计,间距为L,导轨平面与磁场方向垂直。ab、cd为两根垂直导轨放置的、电阻都为R、质量都为m的金属棒。棒cd用能承受最大拉力为T0的水平细线拉住,棒cd与导轨间的最大静摩擦力为f 。棒ab与导轨间的摩擦不计,在水平拉力F的作用下以加速度a由静止开始向右做匀加速直线运动,求: