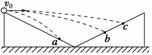
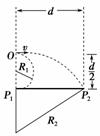
9.横截面为直角三角形的两个相同斜面紧靠在一起,固定在
|
长的一半.现有三个小球从左边斜面的顶点以不同的初速度向右平抛,最后落在斜面
上.其落点分别是a、b、c.下列判断正确的是( )
A.图中三小球比较,落在a点的小球飞行时间最短
B.图中三小球比较,落在c点的小球飞行过程速度变化最大
C.图中三小球比较,落在c点的小球飞行过程速度变化最快
 D.无论小球抛出时初速度多大,落到两个斜面上的瞬时速度都不可能与斜面垂直
D.无论小球抛出时初速度多大,落到两个斜面上的瞬时速度都不可能与斜面垂直
解析:如图所示,由于小球在平抛运动过程中,可分解为
竖直方向的自由落体运动和水平方向的匀速直线运动,由
于竖直方向的位移为落在c点处的最小,而落在a点处的最大,所以落在a点的小球飞行时间最长,A错误;而速度的变化量Δv=gt,所以落在c点的小球速度变化最小,B错误;三个小球做平抛运动的加速度都为重力加速度,故三个小球飞行过程中速度变化一样快,C错误;因为平抛运动可等效为从水平位移中点处做直线运动,故小球不可能垂直落到左边的斜面上.假设小球落在右边斜面的b点处的速度与斜面垂直,则tan θ==,由于两斜面的竖直边是底边长的一半,故小球落在左边斜面最低点处时,因为2x=v0t,x=t,所以vym=v0,而vy≤vym,所以tan θ=≥1,与假设矛盾,故在右边斜面上,小球也不可能垂直落在斜面上,D正确.
答案:D
6.(2010·课标全国,20)太阳系中的8大行星的轨道均可以近似看成圆轨道.下列4幅图是用来描述这些行星运动所遵从的某一规律的图象.图中坐标系的横轴是lg(T/T0),纵轴是lg(R/R0);这里T和R分别是行星绕太阳运行的周期和相应的圆轨道半径,T0和R0分别是水星绕太阳运行的周期和相应的圆轨道半径.下列4幅图中正确的是( )
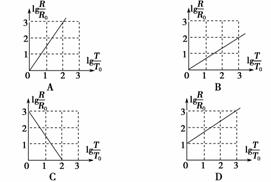
解析:取其中一行星为研究对象,设其质量为m,轨道半径为R,太阳的质量为M,则G=m2·R,得=,水星=.所以3=2,所以3lg=2lg.
答案:B
|
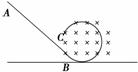 7.如图1-3-18所示,ABC为竖直平面内的光滑绝缘轨道,其中
7.如图1-3-18所示,ABC为竖直平面内的光滑绝缘轨道,其中
AB为倾斜直轨道,BC为与AB相切的圆形轨道,并且圆形轨道
处在匀强磁场中,磁场方向垂直纸面向里.质量相同的甲、乙、
丙三个小球中,甲球带正电、乙球带负电、丙球不带电.现将三个小球在轨道AB上分
别从不同高度处由静止释放,都恰好通过圆形轨道的最高点,则( )
A.经过最高点时,三个小球的速度相等
B.经过最高点时,甲球的速度最小
C.甲球的释放位置比乙球的高
D.运动过程中三个小球的机械能均保持不变
解析:三个粒子在运动过程中机械能守恒,对甲有qv1B+mg=,对乙有mg-qv2B=,对丙有mg=,可判断A、B错,C、D对.
答案:CD
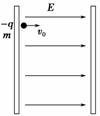
|
靠近左板处有一带电量为-q、质量为m的小球,以水平初速度v0
向右射出.已知在运动过程中不与右板发生碰撞,也没有落地.若
重力加速度为g,不计空气阻力,则( )
A.在碰到左板前,小球做匀变速直线运动
B.两板之间的距离d>mv02/2qE
C.根据题干所给的条件,可以求得小球回到出发点的正下方时速度的大小和方向
D.小球向右运动时下落的高度与向左运动时下落的高度之比为1∶2
解析:对小球受力分析知,小球在水平方向做匀减速直线运动,在竖直方向做自由落体运动,运动轨迹为曲线,A错;水平方向Eq=ma,0-v02=-2ax,x=,要使小球不与右板碰撞,则d>x,B对;回到出发点的正下方时水平速率为v0,方向水平向左,运动时间为t==,竖直速度vy=gt=,可求出此时的速度,C对;小球向右运动和向左运动的时间相等,两段时间内的竖直方向位移之比为1∶3,D错.
 答案:BC
答案:BC
3.在我国乒乓球运动有广泛的群众基础,并有“国球”的美誉,在2008年北京奥运会上中国选手包揽了四个项目的全部冠军.现讨论乒乓球发球问题,已知球台长L、网高h,若球在球台边缘O点正上方某高度处,以一定的垂直球网的水平速度发出,如图1-3-15所示,球恰好在最高点时刚好越过球网.假设乒乓球反弹前后水平分速度不变,竖直分速度大小不变、方向相反,且不考虑乒乓球的旋转和空气阻力.则根据以上信息可以求出(设重力加速度为g)( )
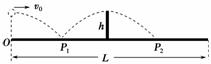
图1-3-15
A.球的初速度大小
B.发球时的高度
C.球从发出到第一次落在球台上的时间
D.球从发出到被对方运动员接住的时间
解析:根据题意分析可知,乒乓球在球台上的运动轨迹具有对称性,显然发球时的高度等于h,从发球到运动到P1点的水平位移等于L,所以可以求出球的初速度大小,也可以求出球从发出到第一次落在球台上的时间.由于对方运动员接球的位置未知,所以无法求出球从发出到被对方运动员接住的时间.
 答案:ABC
答案:ABC
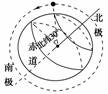
|
道可视为圆轨道).若已知一个极地卫星从北纬30°的正上方,按图示
方向第一次运行至南纬60°正上方时所用时间为t,地球半径为R(地球可看做球体),地 球表面的重力加速度为g,引力常量为G.由以上条件可以求出( )
A.卫星运行的周期 B.卫星距地面的高度
C.卫星的质量 D.地球的质量
解析:本题考查万有引力定律、圆周运动相关公式的应用能力.卫星从北纬30°的正上方,第一次运行至南纬60°正上方时,刚好为运动周期的,所以卫星运行的周期为4t,A项正确;知道周期、地球的半径,由=m2(R+h),可以算出卫星距地面的高度,B项正确;通过上面的公式可以看出,只能算出中心天体的质量,C项错误,D项正确.
答案:ABD
|
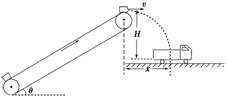
 5.投飞镖是深受人们喜爱的一种娱乐活动.如图1-3-17所示,某
5.投飞镖是深受人们喜爱的一种娱乐活动.如图1-3-17所示,某
同学将一枚飞镖从高于靶心的位置水平投向竖直悬挂的靶盘,结
果飞镖打在靶心的正下方.忽略飞镖运动过程中所受空气阻力,
在其他条件不变的情况下,为使飞镖命中靶心,他在下次投掷时应该( )
A.换用质量稍大些的飞镖
B.适当减小投飞镖时的高度
C.到稍远些的地方投飞镖
D.适当增大投飞镖的初速度
解析:在不计空气阻力的情况下,飞镖做的是平抛运动,水平位移x=v0t,竖直位移y=gt2,联立消去时间t得y=x2,可知打不中靶心与飞镖的质量无关,选项A错;由题意知,飞镖打在靶心的正下方,要想命中靶心,即使y减小,故在初速度v0一定时,人应离靶近些;在人离靶的距离x一定时,可增大初速度;在初速度v0和人离靶的距离x一定时,可适当增加投飞镖的高度,故选项B、C错,D正确.
答案:D
1.如图1-3-14所示,中国自主研制的北斗导航系统的“北斗二
号”系列卫星今年起进入组网高峰期,预计在2015年形成覆盖全
球的北斗卫星导航定位系统,将有5颗人造卫星在地球同步轨道
|
时16分,我国在西昌卫星发射中心用“长征三号丙”运载火箭,成功将第二颗北斗导航卫星(COMPASS-G2)送入预定轨道,其轨道低于地球同步轨道.则以下说法正确的是( )
A.若地球同步卫星的轨道半径是地球半径的k倍,则第一宇宙速度是同步卫星运行线速度的k倍
B.若地球同步卫星的轨道半径是地球半径的k倍,则第一宇宙速度是同步卫星运行线速度的倍
C.若地球同步卫星的轨道半径是地球半径的k倍,地球表面附近的重力加速度是同步卫星向心加速度的k倍
D.(COMPASS-G2)的线速度小于同步轨道上运行卫星的线速度
答案:B
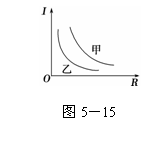 如图5-15是横截面积、长度均相同的甲、乙两根电阻丝的I-R图
如图5-15是横截面积、长度均相同的甲、乙两根电阻丝的I-R图 
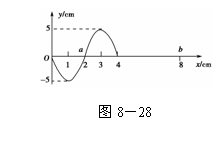 (1)一列简谐横波沿x轴正方向传播,t=0时刻的波形如图8-28所
(1)一列简谐横波沿x轴正方向传播,t=0时刻的波形如图8-28所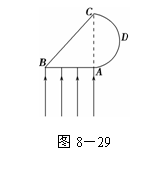 为________ m/s,质点b第一次出现在波峰的时刻为________ s.
为________ m/s,质点b第一次出现在波峰的时刻为________ s. 射出的区域,并求此区域的圆弧长度s.(不考虑经ADC圆弧反射后的
射出的区域,并求此区域的圆弧长度s.(不考虑经ADC圆弧反射后的