3.质量为m的钢球自高处落下,以速率v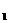 碰地,反弹离地速率为v
碰地,反弹离地速率为v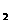 ,则钢球碰地时,地对钢球的冲量为
,则钢球碰地时,地对钢球的冲量为
A.向下,m(v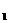 -v
-v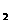 )
B. 向下, m(v
)
B. 向下, m(v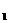 +v
+v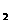 )
)
C.向上, m(v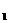 -v
-v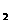 )
D. .向上, m(v
)
D. .向上, m(v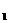 +v
+v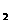 )
)
3.质量为m的钢球自高处落下,以速率v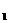 碰地,反弹离地速率为v
碰地,反弹离地速率为v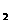 ,则钢球碰地时,地对钢球的冲量为
,则钢球碰地时,地对钢球的冲量为
A.向下,m(v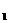 -v
-v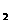 )
B. 向下, m(v
)
B. 向下, m(v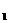 +v
+v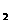 )
)
C.向上, m(v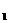 -v
-v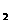 )
D. .向上, m(v
)
D. .向上, m(v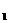 +v
+v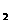 )
)