第二章 函数
一、映射与函数
1.
映射:设A、B是两个集合,如果按照某种对应法则 ,对于集合
,对于集合 的 元素,在集合
的 元素,在集合 中都有 元素与它对应,那么这样的对应叫做
映射,记作:
.
中都有 元素与它对应,那么这样的对应叫做
映射,记作:
.
2.
一一映射:
如果映射 满足:⑴对于
满足:⑴对于 中的不同元素,在集合
中的不同元素,在集合 中有 的象;⑵
中有 的象;⑵ 中的
都有原象,那么
中的
都有原象,那么 叫做
叫做 到
到 的一一映射.
的一一映射.
3.
函数:设A、B是
,如果按某个确定的对应关系 ,对于集合
,对于集合 中
中
的 数 ,在集合
,在集合 中都有 数
中都有 数 和它对应,那么就称
和它对应,那么就称 为集合
为集合 到集合
到集合 一个的函数,记作
一个的函数,记作 ,
, .其中
.其中 叫做
,
叫做
, 的取值范围
的取值范围 叫做函数的 ;与
叫做函数的 ;与 的值相对应的
的值相对应的 的值叫做 ,函数值的集合
的值叫做 ,函数值的集合 叫做函数的
。
叫做函数的
。
4.
区间:设 ,且
,且 ,则区间
,则区间 ={
={ },
},
5. 函数三要素:⑴ ;⑵ ;⑶ .
6. 函数的表示法:⑴ ;⑵ ;⑶ .
7. 分段函数:若函数在定义域的不同子集上有不同的对应法则,可用几个式子来表示函数,这种函数叫做分段函数.
8.
复合函数:若 是
是 的函数,
的函数, 又是
又是 的函数,即:
的函数,即: ,
, ,
, ,
, ,那么
,那么 关于
关于 的函数
的函数 ,
, 叫做
叫做 和
和 的复合函数.
的复合函数.
二、函数的解析式
9、如果一个函数的对应法则可以用一个数学式子来表示,那么这个数学式子就叫函数的解析式.求两个变量的函数关系时,一是求出它们之间的对应法则,二是求出函数的定义域.
10、求解析式的常用方法:
⑴ 已知解析式的结构时,可用待定系数法
⑵ 已知复合函数 的表达式时,可用换元法;
的表达式时,可用换元法;
⑶ 已知抽象函数表达式时,可用消元法.
三、函数的定义域
11、 求定义域时需要考虑:⑴分式的 ;⑵偶次根式的 ;⑶对数式的 ;⑷指数、对数式的 ;⑸由一些基本函数通过四则运算得到解析式使解析式有意义.
12、 已知 的定义域为
的定义域为 ,则
,则 的定义域由
解出;已知
的定义域由
解出;已知 的定义域为
的定义域为 ,则
,则 的定义域为
.
的定义域为
.
四、函数的值域和最值
13、函数的值域取决于函数的对应法则、定义域.
14、求函数值域的常用方法:(写出四种)
1)____________ 2)______________ 3)____________ 4)_______________
15.函数 在区间
在区间 内连续可导,且只有一个点使得
内连续可导,且只有一个点使得 ,若函数在这点处有极大(小)值,则该值是_________________
,若函数在这点处有极大(小)值,则该值是_________________
16.在闭区间 上连续的函数
上连续的函数 在
在 上必有_______________
上必有_______________
五、函数的单调性:
17、定义:
⑴对于给定区间上的函数 ,如果对于这个区间上的任意两个自变量的值
,如果对于这个区间上的任意两个自变量的值 ,当
,当 时都有 ,那么就说
时都有 ,那么就说 是这个区间上的增函数;
是这个区间上的增函数;
⑵对于给定区间上的函数 ,如果对于这个区间上的任意两个自变量的值
,如果对于这个区间上的任意两个自变量的值 ,当
,当 时都有 ,那么就说
时都有 ,那么就说 是这个区间上的减函数.
是这个区间上的减函数.
⑶如果函数 在某个区间上是增函数或减函数,就说函数
在某个区间上是增函数或减函数,就说函数 在这个区间上具有 _____________,这个区间叫做函数
在这个区间上具有 _____________,这个区间叫做函数 的 .
的 .
18、判定:
⑴ 用定义:取值、作差、变形定号、作出结论
⑵ 利用图象;
⑶ 利用复合函数:
写出 的单调区间:
的单调区间:
____________
______________________________________________________________
______________________________________________________________
____________
______________________________________________________________
______________________________________________________________
写出 的单调区间:
的单调区间:
____________
______________________________________________________________
______________________________________________________________
____________
______________________________________________________________
______________________________________________________________
(4)利用导数:函数 在某个区间可导,若
在某个区间可导,若 ,则
,则 在该区间是_________;
在该区间是_________;
若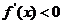 ,则
,则 在该区间是_________。
在该区间是_________。
19、常见函数的单调性:

 时,
时, 在_________上___________
在_________上___________
 时,
时, 在_________上___________
在_________上___________


 时,
时, 在___________________________上___________
在___________________________上___________
 时,
时, 在___________________________上___________
在___________________________上___________



增
增
减
减
20、



增
减
减
增
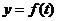
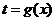

增
增
增
减
减
增
减
减
六、奇函数,偶函数:
21、奇函数:
(1) 定义:①
②
(2) 图象性质:___________________________________
(3) 奇函数在其对称区间上单调性_______
(4) 若0在其定义域内,则 ______
______
22、偶函数:
(1)定义:①
②
(2)图象性质:___________________________________
(3)偶函数在其对称区间上单调性_______
23、奇奇得偶;偶偶得偶;奇偶得奇。
七、周期性:
24、已知函数 的定义域为D,若存在一个非零常数T,使
的定义域为D,若存在一个非零常数T,使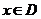 时,都有________________
时,都有________________
则称 为周期函数,_______叫做这个函数的周期。
为周期函数,_______叫做这个函数的周期。
八、反函数:
25、反函数存在的条件:
⑴如果一个函数是________映射,那么这个函数必有反函数.
⑵如果一个函数具有 那么这个函数必有反函数.
26、求反函数的步骤:⑴ ;⑵ ;⑶ .
27、反函数的性质:
(1)互为反函数的两个函数的图象关于 对称;
(2)互为反函数的两个函数在各自的定义域内具有相同的 .
(3)如果一个函数有反函数且为奇函数,那么它的反函数也为_________
九、图象变换
28、对称变换:
①y = f(x)与___________关于x轴对称
②y =f(x)与____________关于y轴对称
③y =f(x)与____________关于原点对称
④若 _____________________,则
_____________________,则 关于__________对称
关于__________对称
29、平移变换:( )
)
 的图象可由
的图象可由 ____________________________________得到
____________________________________得到
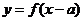 的图象可由
的图象可由 ____________________________________得到
____________________________________得到
 的图象可由
的图象可由 ____________________________________得到
____________________________________得到
 的图象可由
的图象可由 ____________________________________得到
____________________________________得到
30、翻折变换:
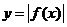 的图象可由
的图象可由 ______________________________________得到
______________________________________得到
 的图象可由
的图象可由 ______________________________________得到
______________________________________得到
十、二次函数
31、函数
1)写出 的顶点式(即配方式)
的顶点式(即配方式) _____________________________
_____________________________
2)若已知 的两根是
的两根是 、
、 ,则
,则 _____________________________
_____________________________
3)单调性:若 ,则
,则 (___________________)时,
(___________________)时, 单调递减
单调递减
则 (___________________)时,
(___________________)时, 单调递增
单调递增
若 ,则
,则 (___________________)时,
(___________________)时, 单调递减
单调递减
则 (___________________)时,
(___________________)时, 单调递增
单调递增
4)讨论 在闭区间
在闭区间 上的最值 (
上的最值 ( )
)
①
②
③
5)讨论 的根在某区间上的分布情况 (
的根在某区间上的分布情况 ( )
)
①在区间 上有且仅有一根,则_________________________________
上有且仅有一根,则_________________________________
②在区间 上有两根,则_____________________________________________________
上有两根,则_____________________________________________________
③在区间 、
、 上各有一根,则______________________________
上各有一根,则______________________________
十一、指数:
32、整数指数幂概念:


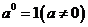
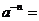 ________
________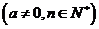
33、 的
的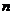 次方根的概念
次方根的概念
一般地,如果一个数的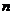 次方等于
次方等于
 ,那么这个数叫做
,那么这个数叫做 的
的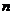 次方根,
次方根,
即: 若 ,则
,则 叫做
叫做 的
的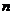 次方根,
次方根, 
说明: ①若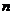 是奇数,则
是奇数,则 的
的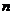 次方根记作
次方根记作 ; 若
; 若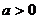 则
则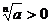 ,若
,若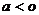 则
则 ;
;
②若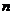 是偶数,且
是偶数,且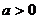 ,则
,则 的正
的正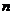 次方根记作
次方根记作 ,
, 的负
的负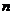 次方根,记作:
次方根,记作: ;
;
③若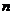 是偶数,且
是偶数,且 ,则
,则 没意义,即负数没有偶次方根;
没意义,即负数没有偶次方根;
④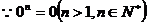 ∴
∴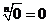 ;
;
⑤式子 叫根式,
叫根式,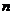 叫根指数,
叫根指数, 叫被开方数。 ∴
叫被开方数。 ∴ .
.
34、 的
的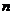 次方根的性质
次方根的性质
一般地,若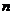 是奇数,则
是奇数,则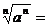 ;
;
若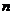 是偶数,则
是偶数,则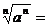 ________。
________。
35、分数指数幂:
(1)正数的正分数指数幂的意义是
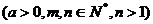 ;
;
(2)正数的负分数指数幂的意义是 =
= 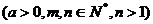 .
.
36、分数指数幂的运算性质:整数指数幂的运算性质对于分数指数幂也同样适用
即
(1) 
 (2)
(2) 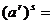

(3) 

说明:(1)有理数指数幂的运算性质对无理数指数幂同样适用;
(2)0的正分数指数幂等于0,0的负分数指数幂没意义。
十二、指数函数:
37、指数函数定义: 一般地,函数 (
( 且
且 )叫做指数函数,其中
)叫做指数函数,其中 是自变量。
是自变量。
38、指数函数 在底数
在底数 及
及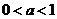 这两种情况下的图象和性质:
这两种情况下的图象和性质:

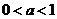
图象
性质
(1)定义域:
(2)值域:
(3)过点( , ) ,
当 时,
时, _____;
_____;
当 时,
时, _____;
_____;
 越___,图象越靠近_________
越___,图象越靠近_________
(3)过点( , ) ,
当 时,
时, _____;
_____;
当 时,
时, _____;
_____;
 越___,图象越靠近_________
越___,图象越靠近_________
(4)单调性:在 上是 函数
(4)单调性:在 上是 函数
十三、对数
39、对数定义:一般地,如果 (
( )的
)的 次幂等于N, 就是
次幂等于N, 就是 ,那么数 b叫做a为底 N的对数,记作
,那么数 b叫做a为底 N的对数,记作  ,a叫做对数的底数,N叫做真数。
,a叫做对数的底数,N叫做真数。
即
 。
。
说明:1.在指数式中幂N > 0,∴在对数式中,真数N > 0.(负数与零没有对数)
2.对任意 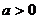 且
且  , 都有
, 都有  ∴
∴ _______,
_______, _______.
_______.
3.如果把 中的
中的 写成
写成 , 则有
, 则有  __________(对数恒等式).
__________(对数恒等式).
4.两种特殊的对数:
①常用对数:以10作底 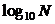 写成
写成 
②自然对数:以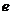 作底为无理数,
作底为无理数,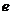 = 2.71828…… ,
= 2.71828…… ,  写成
写成  .
.
40、对数的运算性质:
如果 a > 0 , a ¹ 1, M > 0 ,N > 0,那么 (1) ;
;
(2) ;
(3)
;
(3)
 .
.
41、换底公式: ( a > 0 , a ¹ 1 ;
( a > 0 , a ¹ 1 ; )
)
说明:两个较为常用的推论:
(1) ____; (2)
____; (2) (
( 、
、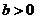 且均不为1).
且均不为1).
十四、对数函数
42、对数函数的定义:一般地,函数 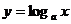
 叫做对数函数,其中
叫做对数函数,其中 是自
是自
变量。
43、对数函数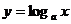 在底数
在底数 及
及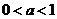 这两种情况下的图象和性质列表:
这两种情况下的图象和性质列表:
图
象

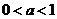
性
质
(1)定义域:
(2)值域:
(3)过点( , ),
当 时,
时, _____;
_____;
当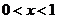 时,
时, _____;
_____;
 越___,图象越靠近_________
越___,图象越靠近_________
(3)过点( , ),
当 时,
时, _____;
_____;
当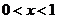 时,
时, _____;
_____;
 越___,图象越靠近_________
越___,图象越靠近_________
(4)单调性:在______上是 函数
(4)单调性:在______上是 函数