摘要:说明:1.在指数式中幂N > 0.∴在对数式中.真数N > 0.(负数与零没有对数)
网址:http://m.1010jiajiao.com/timu_id_172130[举报]
计算
+2
+3
+…+n
,可以采用以下方法:构造恒等式
+
x+
x2+…+
xn=(1+x)n,两边对x求导,得
+2
x+3
x2+…+n
xn-1=n(1+x)n-1,在上式中令x=1,得
+2
+3
+…+n
=n•2n-1.类比上述计算方法,计算
+22
+32
+…+n2
=
查看习题详情和答案>>
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
n(n+1)•2n-2
n(n+1)•2n-2
.计算
+2
+3
+…+n
,可以采用以下方法:构造恒等式
+
x+
x2+…+
xn=(1+x)n,两边对x求导,得
+2
x+3
x2+…+n
xn-1=n(1+x)n-1,在上式中令x=1,得
+2
+3
+…+n
=n•2n-1.类比上述计算方法,计算
+22
+32
+…+n2
=______.
查看习题详情和答案>>
| C | 1n |
| C | 2n |
| C | 3n |
| C | nn |
| C | 0n |
| C | 1n |
| C | 2n |
| C | nn |
| C | 1n |
| C | 2n |
| C | 3n |
| C | nn |
| C | 1n |
| C | 2n |
| C | 3n |
| C | nn |
| C | 1n |
| C | 2n |
| C | 3n |
| C | nn |
给出下列结论:
(1)在回归分析中,可用指数系数R2的值判断模型的拟合效果,R2越大,模型的拟合效果越好;
(2)在回归分析中,可用残差平方和判断模型的拟合效果,残差平方和越大,模型的拟合效果越好;
(3)在回归分析中,可用相关系数r的值判断模型的拟合效果,r越大,模型的拟合效果越好;
(4)在回归分析中,可用残差图判断模型的拟合效果,残差点比较均匀地落在水平的带状区域中,说明这样的模型比较合适.带状区域的宽度越窄,说明模型的拟合精度越高.
以上结论中,正确的有( )个.
(1)在回归分析中,可用指数系数R2的值判断模型的拟合效果,R2越大,模型的拟合效果越好;
(2)在回归分析中,可用残差平方和判断模型的拟合效果,残差平方和越大,模型的拟合效果越好;
(3)在回归分析中,可用相关系数r的值判断模型的拟合效果,r越大,模型的拟合效果越好;
(4)在回归分析中,可用残差图判断模型的拟合效果,残差点比较均匀地落在水平的带状区域中,说明这样的模型比较合适.带状区域的宽度越窄,说明模型的拟合精度越高.
以上结论中,正确的有( )个.
查看习题详情和答案>>
 的值判断模型的拟合效果,
的值判断模型的拟合效果, 的值判断模型的拟合效果,
的值判断模型的拟合效果, 的值判断模型的拟合效果,
的值判断模型的拟合效果,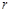 的值判断模型的拟合效果,
的值判断模型的拟合效果,