摘要:若.则时.单调递减
网址:http://m.1010jiajiao.com/timu_id_172092[举报]
已知函数 ,(
,(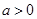 ),
),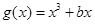
(1)若曲线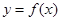 与曲线
与曲线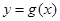 在它们的交点(1,c)处具有公共切线,求a,b的值
在它们的交点(1,c)处具有公共切线,求a,b的值
(2)当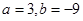 时,若函数
时,若函数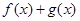 在区间[k,2]上的最大值为28,求k的取值范围
在区间[k,2]上的最大值为28,求k的取值范围
【解析】(1)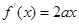 ,
,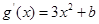
∵曲线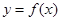 与曲线
与曲线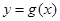 在它们的交点(1,c)处具有公共切线
在它们的交点(1,c)处具有公共切线
∴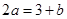 ,
,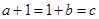
∴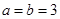
(2)当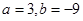 时,
时,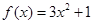 ,
,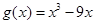 ,
,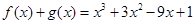
令 ,则
,则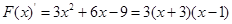 ,令
,令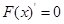 ,
, ∴
∴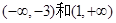 为单调递增区间,
为单调递增区间,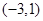 为单调递减区间,其中F(-3)=28为极大值,所以如果区间[k,2]最大值为28,即区间包含极大值点
为单调递减区间,其中F(-3)=28为极大值,所以如果区间[k,2]最大值为28,即区间包含极大值点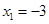 ,所以
,所以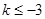
【考点定位】此题应该说是导数题目中较为常规的类型题目,考查的切线,单调性,极值以及最值问题都是课本中要求的重点内容,也是学生掌握比较好的知识点,在题目中能够发现F(-3)=28,和分析出区间[k,2]包含极大值点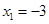 ,比较重要
,比较重要
查看习题详情和答案>>
探究函数f(x)=x+
,x∈(0,+∞)的最小值,并确定相应的x的值,列表如下:
请观察表中y值随x值变化的特点,完成下列问题:
(1)若x1x2=4,则f(x1)
,(x>0)在区间(0,2)上递减,则在区间
(2)当x=
,(x>0)的最小值为
(3)试用定义证明f(x)=x+
,在区间(0,2)上单调递减.
查看习题详情和答案>>
| 4 |
| x |
| x | … |
|
|
1 |
|
2 |
|
4 | 8 | 16 | … | ||||||||
| y | … | 16.25 | 8.5 | 5 |
|
4 |
|
5 | 8.5 | 16.25 | … |
(1)若x1x2=4,则f(x1)
=
=
f(x2)(请填写“>,=,<”号);若函数f(x)=x+| 4 |
| x |
(2,+∞)
(2,+∞)
上递增;(2)当x=
2
2
时,f(x)=x+| 4 |
| x |
4
4
;(3)试用定义证明f(x)=x+
| 4 |
| x |


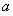
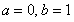

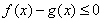

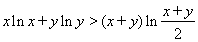
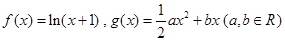 .
.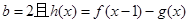 存在单调递减区间,求实数
存在单调递减区间,求实数 的取值范围;
的取值范围;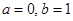 ,求证:当
,求证:当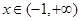 时,
时,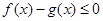 恒成立;
恒成立;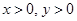 ,则
,则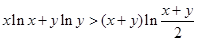 .
.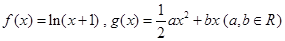 .
.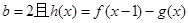 存在单调递减区间,求实数
存在单调递减区间,求实数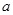 的取值范围;
的取值范围; ,求证:当
,求证:当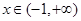 时,
时,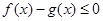 恒成立;
恒成立;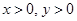 ,则
,则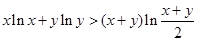 .
.