摘要：反函数的性质:(1)互为反函数的两个函数的图象关于 对称,(2)互为反函数的两个函数在各自的定义域内具有相同的 ．(3)如果一个函数有反函数且为奇函数.那么它的反函数也为 九.图象变换
网址：http://m.1010jiajiao.com/timu_id_172076[举报]
我们知道：两个互为反函数的函数y=2x与y=log2x的图象关于直线y=x成轴对称，利这一性质，若x1和x2分别是2x+x+a=0和log2x+x+a=0的两根，则x1+x2的值为直线y=x与直线y=-x-a的交点的横坐标的2倍，即x1+x2=-a； 由函数y=x3与函数y=
互为反函数，我们可以得出：若方程x3+x-3=0的根为x1，方程（x-3）3+x=0的根为x2，则x1+x2=
查看习题详情和答案>>
| 3 | x |
3
3
．我们知道：两个互为反函数的函数y=2x与y=log2x的图象关于直线y=x成轴对称，利这一性质，若x1和x2分别是2x+x+a=0和log2x+x+a=0的两根，则x1+x2的值为直线y=x与直线y=-x-a的交点的横坐标的2倍，即x1+x2=-a； 由函数y=x3与函数y=
互为反函数，我们可以得出：若方程x3+x-3=0的根为x1，方程（x-3）3+x=0的根为x2，则x1+x2=______．
查看习题详情和答案>>
| 3 | x |
我们知道：两个互为反函数的函数y=2x与y=log2x的图象关于直线y=x成轴对称，利这一性质，若x1和x2分别是2x+x+a=0和log2x+x+a=0的两根，则x1+x2的值为直线y=x与直线y=-x-a的交点的横坐标的2倍，即x1+x2=-a； 由函数y=x3与函数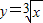
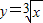互为反函数，我们可以得出：若方程x3+x-3=0的根为x1，方程（x-3）3+x=0的根为x2，则x1+x2= ．
查看习题详情和答案>>
互为反函数，我们可以得出：若方程x3+x-3=0的根为x1，方程（x-3）3+x=0的根为x2，则x1+x2= ．
查看习题详情和答案>>
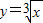互为反函数，我们可以得出：若方程x3+x-3=0的根为x1，方程（x-3）3+x=0的根为x2，则x1+x2= ．
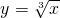互为反函数，我们可以得出：若方程x3+x-3=0的根为x1，方程（x-3）3+x=0的根为x2，则x1+x2=________．