摘要:对称变换:①y = f(x)与 关于x轴对称②y =f(x)与 关于y轴对称③y =f(x)与 关于原点对称
网址:http://m.1010jiajiao.com/timu_id_172077[举报]
定义:若函数f(x)的图象经过变换T后所得图象对应函数的值域与f(x)的值域相同,则称变换T是f(x)的同值变换.下面给出四个函数及其对应的变换T,其中T不属于f(x)的同值变换的是( )
A.f(x)=(x-1)2,T将函数f(x)的图象关于y轴对称
B.f(x)=2x-1-1,T将函数f(x)的图象关于x轴对称
C.f(x)=2x+3,T将函数f(x)的图象关于点(-1,1)对称
D. ,T将函数f(x)的图象关于点(-1,0)对称
,T将函数f(x)的图象关于点(-1,0)对称
查看习题详情和答案>>
A.f(x)=(x-1)2,T将函数f(x)的图象关于y轴对称
B.f(x)=2x-1-1,T将函数f(x)的图象关于x轴对称
C.f(x)=2x+3,T将函数f(x)的图象关于点(-1,1)对称
D.
 ,T将函数f(x)的图象关于点(-1,0)对称
,T将函数f(x)的图象关于点(-1,0)对称查看习题详情和答案>>
定义:若函数f(x)的图象经过变换T后所得图象对应函数的值域与f(x)的值域相同,则称变换T是f(x)的同值变换.下面给出四个函数及其对应的变换T,其中T不属于f(x)的同值变换的是( )
A.f(x)=(x-1)2,T将函数f(x)的图象关于y轴对称
B.f(x)=2x-1-1,T将函数f(x)的图象关于x轴对称
C.f(x)=2x+3,T将函数f(x)的图象关于点(-1,1)对称
D. ,T将函数f(x)的图象关于点(-1,0)对称
,T将函数f(x)的图象关于点(-1,0)对称
查看习题详情和答案>>
A.f(x)=(x-1)2,T将函数f(x)的图象关于y轴对称
B.f(x)=2x-1-1,T将函数f(x)的图象关于x轴对称
C.f(x)=2x+3,T将函数f(x)的图象关于点(-1,1)对称
D.
 ,T将函数f(x)的图象关于点(-1,0)对称
,T将函数f(x)的图象关于点(-1,0)对称查看习题详情和答案>>
定义:若函数f(x)的图象经过变换T后所得图象对应的函数与f(x)的值域相同,则称变换T是f(x)的同值变换。下面给出了四个函数与对应的变换:
①f(x)=(x-1)2,T:将函数f(x)的图象关于y轴对称;
② ,T:将函数f(x)的图象关于x轴对称;
,T:将函数f(x)的图象关于x轴对称;
③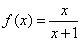 ,T:将函数f(x)的图象关于点(-1,1)对称;
,T:将函数f(x)的图象关于点(-1,1)对称;
④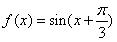 ,T:将函数f(x)的图象关于点(-1,0)对称;
,T:将函数f(x)的图象关于点(-1,0)对称;
其中T是f(x)的同值变换的有( )(写出所有符合题意的序号)。
查看习题详情和答案>>
①f(x)=(x-1)2,T:将函数f(x)的图象关于y轴对称;
②
 ,T:将函数f(x)的图象关于x轴对称;
,T:将函数f(x)的图象关于x轴对称;③
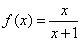 ,T:将函数f(x)的图象关于点(-1,1)对称;
,T:将函数f(x)的图象关于点(-1,1)对称;④
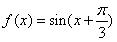 ,T:将函数f(x)的图象关于点(-1,0)对称;
,T:将函数f(x)的图象关于点(-1,0)对称;其中T是f(x)的同值变换的有( )(写出所有符合题意的序号)。
给出下列四个命题:
①“向量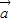 ,
,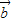 的夹角为锐角”的充要条件是“
的夹角为锐角”的充要条件是“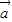 •
• >0”;
>0”;
②如果f(x)=lgx,则对任意的x1、x2∈(0,+∞),且x1≠x2,都有f(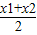 )>
)>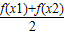 ;
;
③设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若对任意x∈[a,b],都有|f(x)-g(x)|≤1成立,则称f(x)和g(x)在[a,b]上是“密切函数”,区间[a,b]称为“密切区间”.若f(x)=x2-3x+4与g(x)=2x-3在[a,b]上是“密切函数”,则其“密切区间”可以是[2,3];
④记函数y=f(x)的反函数为y=f-1(x),要得到y=f-1(1-x)的图象,可以先将y=f(x)的图象关于直线y=x做对称变换,再将所得的图象关于y轴做对称变换,再将所得的图象沿x轴向左平移1个单位,即得到y=f-1(1-x)的图象.
其中真命题的序号是 .(请写出所有真命题的序号) 查看习题详情和答案>>
①“向量
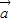 ,
,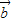 的夹角为锐角”的充要条件是“
的夹角为锐角”的充要条件是“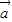 •
• >0”;
>0”;②如果f(x)=lgx,则对任意的x1、x2∈(0,+∞),且x1≠x2,都有f(
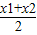 )>
)>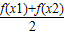 ;
;③设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若对任意x∈[a,b],都有|f(x)-g(x)|≤1成立,则称f(x)和g(x)在[a,b]上是“密切函数”,区间[a,b]称为“密切区间”.若f(x)=x2-3x+4与g(x)=2x-3在[a,b]上是“密切函数”,则其“密切区间”可以是[2,3];
④记函数y=f(x)的反函数为y=f-1(x),要得到y=f-1(1-x)的图象,可以先将y=f(x)的图象关于直线y=x做对称变换,再将所得的图象关于y轴做对称变换,再将所得的图象沿x轴向左平移1个单位,即得到y=f-1(1-x)的图象.
其中真命题的序号是 .(请写出所有真命题的序号) 查看习题详情和答案>>
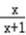 ,T3将函数f(x)的图象关于点(﹣1,1)对称;
,T3将函数f(x)的图象关于点(﹣1,1)对称; ),T4将函数f(x)的图象关于点(﹣1,0)对称.
),T4将函数f(x)的图象关于点(﹣1,0)对称.