2009年高考数学总复习解题思维专题讲座之三
数学思维的严密性
一、概述
在中学数学中,思维的严密性表现为思维过程服从于严格的逻辑规则,考察问题时严格、准确,进行运算和推理时精确无误。数学是一门具有高度抽象性和精密逻辑性的科学,论证的严密性是数学的根本特点之一。但是,由于认知水平和心里特征等因素的影响,中学生的思维过程常常出现不严密现象,主要表现在以下几个方面:
概念模糊 概念是数学理论体系中十分重要的组成部分。它是构成判断、推理的要素。因此必须弄清概念,搞清概念的内涵和外延,为判断和推理奠定基础。概念不清就容易陷入思维混乱,产生错误。
判断错误 判断是对思维对象的性质、关系、状态、存在等情况有所断定的一种思维形式。数学中的判断通常称为命题。在数学中,如果概念不清,很容易导致判断错误。例如,“函数 是一个减函数”就是一个错误判断。
是一个减函数”就是一个错误判断。
推理错误 推理是运用已知判断推导出新的判断的思维形式。它是判断和判断的联合。任何一个论证都是由推理来实现的,推理出错,说明思维不严密。
例如,解不等式
解 
 或
或  这个推理是错误的。在由
这个推理是错误的。在由 推导
推导 时,没有讨论
时,没有讨论 的正、负,理由不充分,所以出错。
的正、负,理由不充分,所以出错。
二、思维训练实例
例1、
不等式 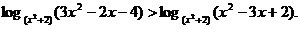
错误解法 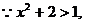


错误分析 当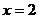 时,真数
时,真数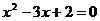 且
且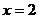 在所求的范围内(因
在所求的范围内(因 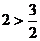 ),说明解法错误。原因是没有弄清对数定义。此题忽视了“对数的真数大于零”这一条件造成解法错误,表现出思维的不严密性。
),说明解法错误。原因是没有弄清对数定义。此题忽视了“对数的真数大于零”这一条件造成解法错误,表现出思维的不严密性。
正确解法 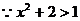
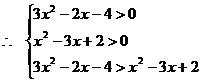

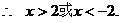
例2、
求过点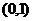 的直线,使它与抛物线
的直线,使它与抛物线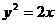 仅有一个交点。
仅有一个交点。
错误解法 设所求的过点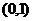 的直线为
的直线为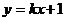 ,则它与抛物线的交点为
,则它与抛物线的交点为
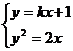 ,消去
,消去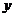 得:
得: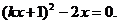
整理得
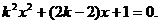
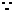 直线与抛物线仅有一个交点,
直线与抛物线仅有一个交点,
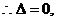 解得
解得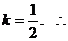 所求直线为
所求直线为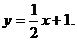
错误分析 此处解法共有三处错误:
第一,设所求直线为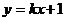 时,没有考虑
时,没有考虑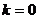 与斜率不存在的情形,实际上就是承认了该直线的斜率是存在的,且不为零,这是不严密的。
与斜率不存在的情形,实际上就是承认了该直线的斜率是存在的,且不为零,这是不严密的。
第二,题中要求直线与抛物线只有一个交点,它包含相交和相切两种情况,而上述解法没有考虑相切的情况,只考虑相交的情况。原因是对于直线与抛物线“相切”和“只有一个交点”的关系理解不透。
第三,将直线方程与抛物线方程联立后得一个一元二次方程,要考虑它的判别式,所以它的二次项系数不能为零,即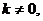 而上述解法没作考虑,表现出思维不严密。
而上述解法没作考虑,表现出思维不严密。
正确解法 当所求直线斜率不存在时,即直线垂直 轴,因为过点
轴,因为过点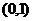 ,所以
,所以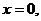 即
即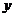 轴,它正好与抛物线
轴,它正好与抛物线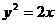 相切。
相切。
当所求直线斜率为零时,直线为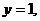 平行
平行 轴,它正好与抛物线
轴,它正好与抛物线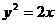 只有一个交点。
只有一个交点。
设所求的过点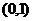 的直线为
的直线为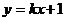
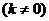 则
则
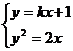 ,
,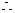
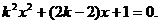 令
令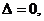 解得
解得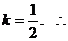 所求直线为
所求直线为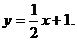
综上,满足条件的直线为:

(2) 判断的训练
造成判断错误的原因很多,我们在学习中,应重视如下几个方面。
①注意定理、公式成立的条件
数学上的定理和公式都是在一定条件下成立的。如果忽视了成立的条件,解题中难免出现错误。
例3、
实数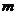 ,使方程
,使方程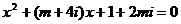 至少有一个实根。
至少有一个实根。
错误解法 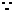 方程至少有一个实根,
方程至少有一个实根,
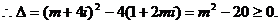
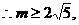 或
或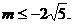
错误分析 实数集合是复数集合的真子集,所以在实数范围内成立的公式、定理,在复数范围内不一定成立,必须经过严格推广后方可使用。一元二次方程根的判别式是对实系数一元二次方程而言的,而此题目盲目地把它推广到复系数一元二次方程中,造成解法错误。
正确解法 设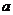 是方程的实数根,则
是方程的实数根,则
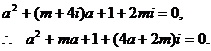
由于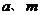 都是实数,
都是实数,

解得
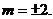
例4 已知双曲线的右准线为 ,右焦点
,右焦点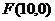 ,离心率
,离心率 ,求双曲线方程。
,求双曲线方程。
错解1 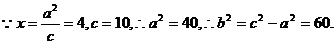
故所求的双曲线方程为
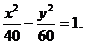
错解2 由焦点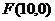 知
知
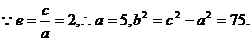
故所求的双曲线方程为
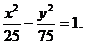
错解分析 这两个解法都是误认为双曲线的中心在原点,而题中并没有告诉中心在原点这个条件。由于判断错误,而造成解法错误。随意增加、遗漏题设条件,都会产生错误解法。
正解1 设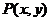 为双曲线上任意一点,因为双曲线的右准线为
为双曲线上任意一点,因为双曲线的右准线为 ,右焦点
,右焦点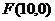 ,离心率
,离心率 ,由双曲线的定义知
,由双曲线的定义知
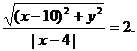
整理得
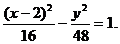
正解2 依题意,设双曲线的中心为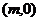
则 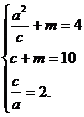 解得
解得 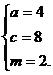
所以 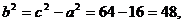
故所求双曲线方程为 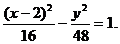
②注意充分条件、必要条件和充分必要条件在解题中的运用
我们知道:
如果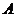 成立,那么
成立,那么 成立,即
成立,即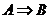 ,则称
,则称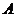 是
是 的充分条件。
的充分条件。
如果 成立,那么
成立,那么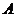 成立,即
成立,即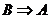 ,则称
,则称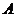 是
是 的必要条件。
的必要条件。
如果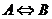 ,则称
,则称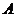 是
是 的充分必要条件。
的充分必要条件。
充分条件和必要条件中我们的学习中经常遇到。像讨论方程组的解,求满足条件的点的轨迹等等。但充分条件和必要条件中解题中的作用不同,稍用疏忽,就会出错。
例5 解不等式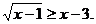
错误解法 要使原不等式成立,只需
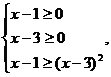 解得
解得
错误分析 不等式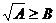 成立的充分必要条件是:
成立的充分必要条件是: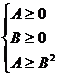 或
或 
原不等式的解法只考虑了一种情况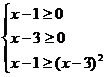 ,而忽视了另一种情况
,而忽视了另一种情况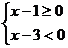 ,所考虑的情况只是原不等式成立的充分条件,而不是充分必要条件,其错误解法的实质,是把充分条件当成了充分必要条件。
,所考虑的情况只是原不等式成立的充分条件,而不是充分必要条件,其错误解法的实质,是把充分条件当成了充分必要条件。
正确解法 要使原不等式成立,则
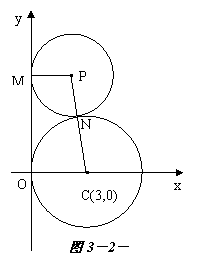
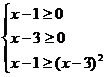 或
或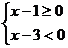
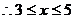 ,或
,或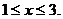
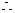 原不等式的解集为
原不等式的解集为 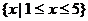
例6(轨迹问题)求与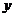 轴相切于右侧,并与
轴相切于右侧,并与
⊙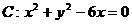 也相切的圆的圆心
也相切的圆的圆心
的轨迹方程。
错误解法 如图3-2-1所示,
已知⊙C的方程为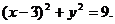
设点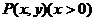 为所求轨迹上任意一点,并且⊙P与
为所求轨迹上任意一点,并且⊙P与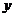 轴相切于M点,
轴相切于M点,
与⊙C相切于N点。根据已知条件得
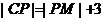 ,即
,即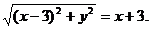
化简得
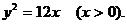
错误分析 本题只考虑了所求轨迹的纯粹性(即所求的轨迹上的点都满足条件),而没有考虑所求轨迹的完备性(即满足条件的点都在所求的轨迹上)。事实上,符合题目条件的点的坐标并不都满足所求的方程。从动圆与已知圆内切,可以发现以 轴正半轴上任一点为圆心,此点到原点的距离为半径(不等于3)的圆也符合条件,所以
轴正半轴上任一点为圆心,此点到原点的距离为半径(不等于3)的圆也符合条件,所以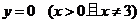 也是所求的方程。即动圆圆心的轨迹方程是
也是所求的方程。即动圆圆心的轨迹方程是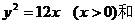
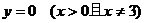 。因此,在求轨迹时,一定要完整的、细致地、周密地分析问题,这样,才能保证所求轨迹的纯粹性和完备性。
。因此,在求轨迹时,一定要完整的、细致地、周密地分析问题,这样,才能保证所求轨迹的纯粹性和完备性。
③防止以偏概全的错误
以偏概全是指思考不全面,遗漏特殊情况,致使解答不完全,不能给出问题的全部答案,从而表现出思维的不严密性。
例7 设等比数列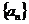 的全
的全 项和为
项和为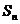 .若
.若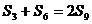 ,求数列的公比
,求数列的公比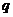 .
.
错误解法 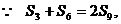

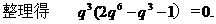
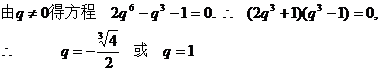
错误分析 在错解中,由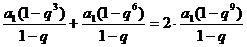
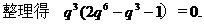 时,应有
时,应有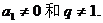 在等比数列中,
在等比数列中,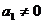 是显然的,但公比
是显然的,但公比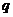 完全可能为1,因此,在解题时应先讨论公比
完全可能为1,因此,在解题时应先讨论公比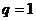 的情况,再在
的情况,再在 的情况下,对式子进行整理变形。
的情况下,对式子进行整理变形。
正确解法 若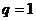 ,则有
,则有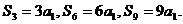
但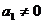 ,即得
,即得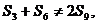 与题设矛盾,故
与题设矛盾,故 .
.
又依题意 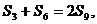
可得
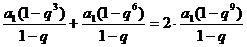
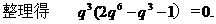 即
即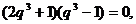
因为 ,所以
,所以 所以
所以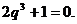
所以

说明 此题为1996年全国高考文史类数学试题第(21)题,不少考生的解法同错误解法,根据评分标准而痛失2分。
④避免直观代替论证
我们知道直观图形常常为我们解题带来方便。但是,如果完全以图形的直观联系为依据来进行推理,这就会使思维出现不严密现象。
 例8 (如图3-2-2),具有公共
例8 (如图3-2-2),具有公共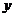 轴的两个直角坐标平面
轴的两个直角坐标平面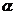 和
和 所成的二面角
所成的二面角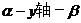 等于
等于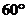 .已知
.已知 内的曲线
内的曲线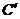 的方程是
的方程是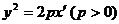 ,求曲线
,求曲线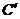 在
在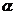 内的射影的曲线方程。
内的射影的曲线方程。
错误解法 依题意,可知曲线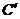 是抛物线,
是抛物线,
在 内的焦点坐标是
内的焦点坐标是
因为二面角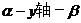 等于
等于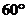 ,
,
且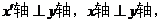 所以
所以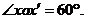
设焦点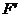 在
在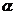 内的射影是
内的射影是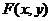 ,那么,
,那么,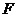 位于
位于 轴上,
轴上,
从而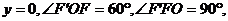
所以 所以点
所以点 是所求射影的焦点。依题意,射影是一条抛物线,开口向右,顶点在原点。
是所求射影的焦点。依题意,射影是一条抛物线,开口向右,顶点在原点。
所以曲线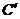 在
在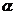 内的射影的曲线方程是
内的射影的曲线方程是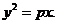
错误分析 上述解答错误的主要原因是,凭直观误认为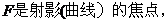
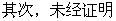
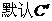
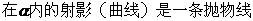 。
。
 正确解法 在
正确解法 在 内,设点
内,设点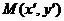 是曲线上任意一点
是曲线上任意一点
(如图3-2-3)过点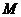 作
作 ,垂足为
,垂足为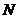 ,
,
过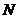 作
作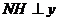 轴,垂足为
轴,垂足为 连接
连接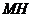 ,
,
则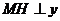 轴。所以
轴。所以 是二面角
是二面角
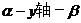 的平面角,依题意,
的平面角,依题意,
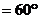 .
.
在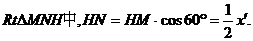
又知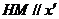 轴(或
轴(或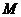 与
与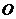 重合),
重合),
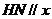 轴(或
轴(或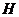 与
与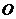 重合),设
重合),设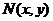 ,
,
则 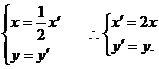
因为点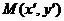 在曲线
在曲线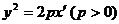 上,所以
上,所以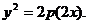
即所求射影的方程为 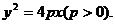
(3) 推理的训练
数学推理是由已知的数学命题得出新命题的基本思维形式,它是数学求解的核心。以已知的真实数学命题,即定义、公理、定理、性质等为依据,选择恰当的解题方法,达到解题目标,得出结论的一系列推理过程。在推理过程中,必须注意所使用的命题之间的相互关系(充分性、必要性、充要性等),做到思考缜密、推理严密。
例9 设椭圆的中心是坐标原点,长轴 在轴上,离心率
在轴上,离心率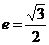 ,已知点
,已知点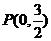 到这个椭圆上的最远距离是
到这个椭圆上的最远距离是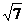 ,求这个椭圆的方程。
,求这个椭圆的方程。
错误解法 依题意可设椭圆方程为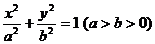
则 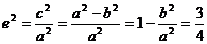 ,
,
所以 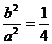 ,即
,即 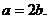
设椭圆上的点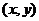 到点
到点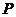 的距离为
的距离为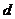 ,
,
则 
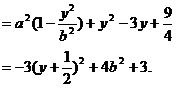
所以当 时,
时,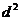 有最大值,从而
有最大值,从而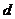 也有最大值。
也有最大值。
所以 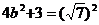 ,由此解得:
,由此解得: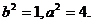
于是所求椭圆的方程为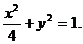
错解分析 尽管上面解法的最后结果是正确的,但这种解法却是错误的。结果正确只是碰巧而已。由当 时,
时,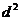 有最大值,这步推理是错误的,没有考虑
有最大值,这步推理是错误的,没有考虑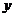 到的取值范围。事实上,由于点
到的取值范围。事实上,由于点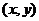 在椭圆上,所以有
在椭圆上,所以有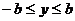 ,因此在求
,因此在求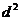 的最大值时,应分类讨论。即:
的最大值时,应分类讨论。即:
若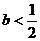 ,则当
,则当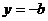 时,
时,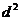 (从而
(从而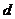 )有最大值。
)有最大值。
于是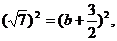 从而解得
从而解得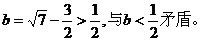
所以必有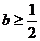 ,此时当
,此时当 时,
时,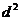 (从而
(从而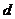 )有最大值,
)有最大值,
所以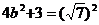 ,解得
,解得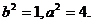
于是所求椭圆的方程为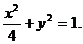
例10 求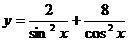 的最小值
的最小值
错解1 
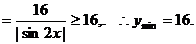
错解2 
错误分析 在解法1中,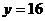 的充要条件是
的充要条件是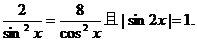
即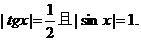 这是自相矛盾的。
这是自相矛盾的。
在解法2中,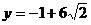 的充要条件是
的充要条件是
 这是不可能的。
这是不可能的。
正确解法1 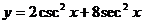
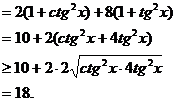
其中,当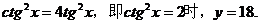
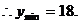
正 确 解 法2 取正常数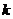 ,易得
,易得
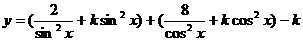
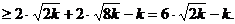
其中“ ”取“=”的充要条件是
”取“=”的充要条件是

因此,当