辽宁省营口市2009届高三高考模拟考试
文科数学试卷
本试卷分第I卷和第II卷两部分。共8页。满分150分。考试时间120分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在试题卷、答题纸及答题卡上,并把答题卡上准考证号对应的位置,用2B铅笔涂黑。座位号填写在答题纸第2页右上角指定位置。
2.选择题每小题选出答案后,用2B铅笔将答题卡上对应题目的答案标号涂黑,如需改动用橡皮擦干净后,再选涂其他答案标号,答在试题卷上无效。
3.非选择题用蓝或黑色笔答在答题纸的答题区域内,答在试题卷上无效。
4.考试结束,请将本试题卷、答题纸和答题卡一并上交。
第I卷
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1、设集合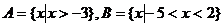 ,则
,则
(A)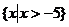 (B)
(B)
(C)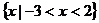 (D)
(D)
2、下列曲线中经过坐标原点的是
(A)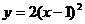 (B)
(B)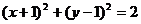
(C)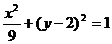 (D)
(D)
 3、若函数
3、若函数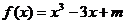 有三个不同的零点,则实数
有三个不同的零点,则实数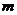 的取值范围是
的取值范围是
(A)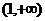 (B)
(B)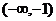
(C) (D)
(D)
4、已知命题 :
: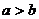 是
是
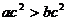 的必要不充分条件;命题
的必要不充分条件;命题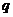 :在
:在 中,
中, 是
是
 的充要条件,则
的充要条件,则
(A) 真
真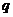 假 (B)
假 (B) 假
假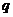 真
真
(C)“ 或
或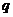 ”为假 (D) “
”为假 (D) “ 且
且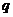 ”为真
”为真
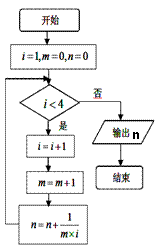
5、右图是一个算法的程序框图,该算法输出
的结果是
(A) (B)
(B)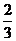
(C)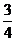 (D)
(D)
6、下列四组函数中,表示同一函数的是
(A)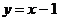 与
与 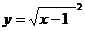 (B)
(B) 与
与 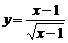
(C)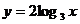 与
与 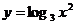 (D)
(D)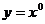 与
与 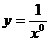
7、如图,用一根铁丝折成一个扇形框架,要求框架所围扇形面积为定值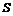 ,半径为
,半径为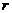 ,弧
,弧
为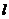 ,则使用铁丝长度最小值时应满足的条件为
,则使用铁丝长度最小值时应满足的条件为
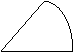 (A)
(A) 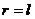 (B)
(B) 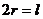
(C) 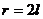 (D)
(D) 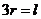
8、若复数 (
(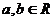 )满足条件
)满足条件 为实数或为纯虚数,则实数
为实数或为纯虚数,则实数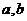 满足的条件是
满足的条件是
(A) 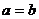 (B)
(B) 
(C) 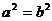 (D)
(D) 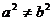
9、一个路口的信号灯,绿灯亮40秒后,黄灯亮若干秒,然后红灯亮30秒,如果一辆车到达路口时,遇到红灯的概率为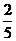 ,那么黄灯亮的时间为
,那么黄灯亮的时间为
(A)3秒 (B)4秒 (C)5秒 (D)6秒
10、已知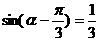 ,则
,则 的值为
的值为
(A)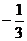 (B)
(B) (C)
(C)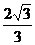 (D)
(D)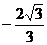
11、向量a、b满足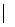 a
a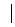 =4,
=4,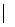 b
b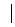 =2且(a-b)
=2且(a-b)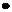 b = 0,则向量a与b的夹角为
b = 0,则向量a与b的夹角为
 (A)
(A)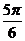 (B)
(B)  (C)
(C) (D)
(D)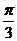
12、如图所示的阴影部分有方格纸上3个小方格组成,
我们称这样的图案为L形(每次旋转 仍为L形
仍为L形
图案),则在由4×5个小方格组成的方格纸上可以
画出不同位置的L形图案的个数是
(A)60 (B)48 (C)36 (D)24
第II卷
(非选择题,共10题 ,90分)
 二、填空题(本大题共4个小题,每小题4分,共16分,答案填在答题纸相应答题区域内)
二、填空题(本大题共4个小题,每小题4分,共16分,答案填在答题纸相应答题区域内)
13、一个几何体的三视图如右图,
则它的表面积为 ××××××× .
14、点 到双曲线
到双曲线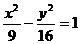 的
的
渐近线的距离是××××××× .
15、函数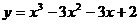 的
的
单调递减区间为××××××× .
16、由不等式组
 所围成的平面区域的面积为××××××× .
所围成的平面区域的面积为××××××× .
三、解答题(本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤)
17、(本小题满分12分)
已知函数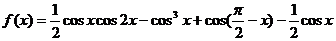
(1)若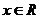 ,求
,求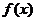 的最大值和最小值;
的最大值和最小值;
(2)若 ,且
,且 ,求
,求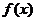 的值.
的值.
18、(本小题满分12分)
设数列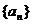 的前
的前 项和为
项和为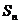 ,如果对于任意的
,如果对于任意的 ,点
,点 都在函数
都在函数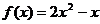 的图像上,且过点
的图像上,且过点 的切线斜率为
的切线斜率为 ,
,
(1)求数列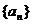 的通项公式;
的通项公式;
(2)若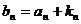 ,求数列
,求数列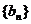 的前前
的前前 项和
项和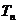 .
.
19、(本小题满分12分)
 如图所示,矩形
如图所示,矩形 中,
中, ⊥平面
⊥平面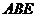 ,
,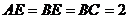 ,
,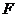 为
为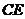 上的点,且
上的点,且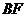 ⊥平面
⊥平面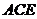 ,
,
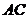 交
交 于点
于点 ,
,
(1)求证: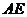 ⊥平面
⊥平面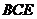 ;
;
(2)求证: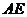 ∥平面
∥平面 ;
;
(3)求三棱锥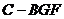 的体积.
的体积.
20、(本小题满分12分)
考察下列式子:
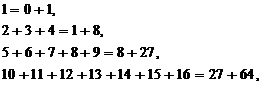
…………………………………………………;
请你做出一般性的猜想,并且证明你猜想的结论。
21、(本小题满分12分)
已知椭圆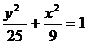 的上、下焦点分别为
的上、下焦点分别为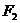 和
和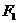 ,点
,点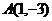 ,
,
(1)在椭圆上有一点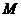 ,使
,使 的值最小,求最小值;
的值最小,求最小值;
(2)当 取最小值时,求三角形
取最小值时,求三角形 的周长.
的周长.
22、(本小题满分14分)
设函数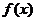 的定义域为
的定义域为 ,当
,当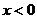 时,
时,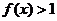 ,且对于任意的实数
,且对于任意的实数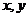 都有
都有
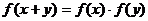 成立,
成立,
(1)求 的值,判断并证明函数
的值,判断并证明函数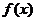 的单调性;
的单调性;
(2)若数列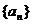 满足
满足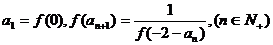 ,求
,求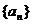 的通项公式;
的通项公式;
(3)如果 ,
,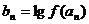 ,求数列
,求数列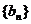 的前
的前 项和
项和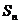 .
.
文科数学试卷答案及评分标准
题 号
1
2
3
4
5
6
7
8
9
10
11
12
正确选项
A
B
D
A
C
D
B
C
C
A
D
B
二、填空题:
13、19375+1250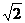 .
14、
.
14、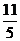 或 1 .
或 1 .
15、 .
16、2
.
.
16、2
.
三、解答题:
17、解: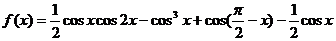

 . ………………2分
. ………………2分
(1)当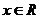 时,
时,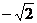 ≤
≤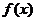 ≤
≤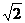 ;
;
∴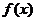 的最大值为
的最大值为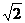 ,最小值为
,最小值为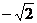 ;……5分
;……5分
(2) 时,
时,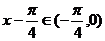 ,
,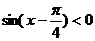
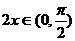 ,
, ;
…………7分
;
…………7分
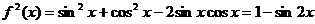 ;
;
 ,则
,则 ;……………9分
;……………9分
∵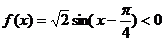
∴ . ………………………12分
. ………………………12分
18、解:由题意得: , ……………………1分
, ……………………1分
(1)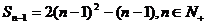 且
且 ≥
≥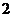 ,可得
,可得
∴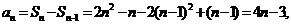 …………3分
…………3分
当 时,
时,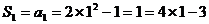
∴数列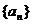 的通项公式为
的通项公式为 . ………………6分
. ………………6分
(2)由题意过点 的切线斜率为
的切线斜率为 ,则
,则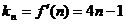
∴ ,……9分
,……9分
∴数列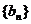 为等差数列,即
为等差数列,即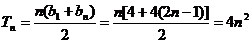
∴数列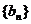 的前
的前 项和为
项和为
 . …………………12分
. …………………12分
19、解:(1)证明:∵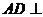 平面
平面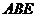 ,
, ∥
∥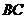 ,
,
 ∴
∴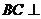 平面
平面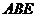 ,则
,则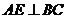 , ……………………2分
, ……………………2分
又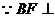 平面
平面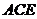 ,则
,则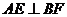
∴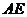 ⊥平面
⊥平面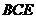 ;…………… 4分
;…………… 4分
(2)由题意可得 是
是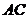 的中点,连接
的中点,连接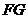
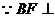 平面
平面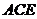 ,则
,则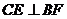 ,
,
而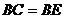 ,∴
,∴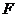 是
是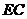 中点
;………6分
中点
;………6分
在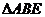 中,
中,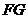 ∥
∥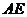 ,∴
,∴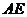 ∥平面
∥平面 . ……………8分
. ……………8分
(3) ∥平面
∥平面 ,∴
,∴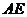 ∥
∥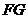 ,
,
而∴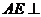 平面
平面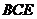 ,∴
,∴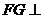 平面
平面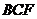
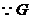 是
是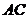 中点,
中点,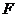 是
是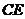 中点,
中点,
∴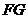 ∥
∥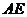 且
且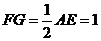 ,
……………………9分
,
……………………9分
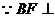 平面
平面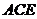 ,∴
,∴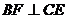 ,
,
∴ 中,
中,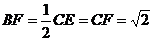 , ………………10分
, ………………10分
∴ …………………………11分
…………………………11分
∴ ………………12分
………………12分
20、解:在椭圆中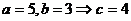 ,
,
∴得到两个焦点为: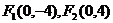 ,
,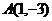 , ……2分
, ……2分
(1) ≥
≥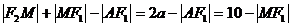 ,
,
当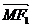 与
与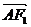 同向共线时取等号,即取最小值; ……4分
同向共线时取等号,即取最小值; ……4分
而 ,
,
∴当点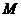 在椭圆上并在线段
在椭圆上并在线段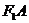 的延长线上时取得最小值,
的延长线上时取得最小值,
 的最小值为
的最小值为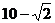 . …………………6分
. …………………6分
(2)当 取得最小值时,点
取得最小值时,点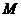 在直线
在直线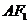 上,
上,
只需求得 即可; …………………………………8分
即可; …………………………………8分
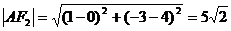 , ……………………10分
, ……………………10分
∴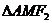 的周长为
的周长为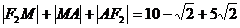
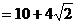 . ……………………………………………12分
. ……………………………………………12分
21、解:猜想: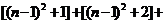 ……
……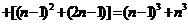
…………………………5分
证明: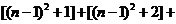 …
…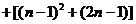
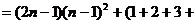 …
…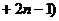 ……7分
……7分
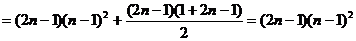
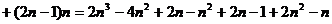
 ……………………………10分
……………………………10分
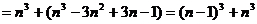 ;………11分
;………11分
∴证明的结论成立,即: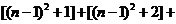
…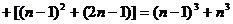 .
…………12分
.
…………12分
22、解:由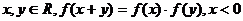 时,
时,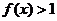 可得:
可得:
(1)令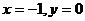 就得
就得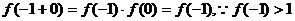 ,
,
∴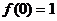 ; ……………………………………………2分
; ……………………………………………2分
若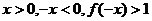 ,则
,则 ,
,
∴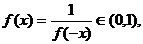 从而的当
从而的当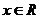 时,
时,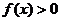 ;………4分
;………4分
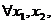 且
且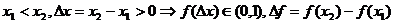
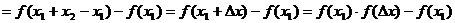
 ;即得
;即得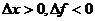 ;
;
∴函数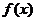 在
在 上是减函数.
…………………………6分
上是减函数.
…………………………6分
(2)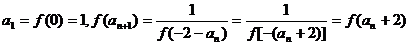
由函数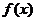 是
是 上单调函数,得
上单调函数,得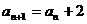 ,
………8分
,
………8分
得到数列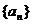 是等差数列,即:
是等差数列,即: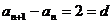 ,又
,又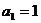
∴ ,即通项公式为
,即通项公式为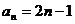 . ……10分
. ……10分
(3)当 ......
......
∴ ,
,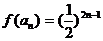 ,因此数列
,因此数列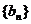 的通项公式为
的通项公式为
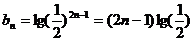 , ……………………………12分
, ……………………………12分
可以得出数列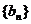 是以
是以 为首项,以
为首项,以 为公差的等差数列,
为公差的等差数列,
∴数列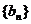 前
前 项和为:
项和为:
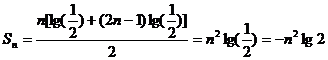 . …………14分
. …………14分