6.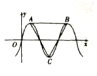 函数$f(x)=3\sqrt{3}sinωx({ω>0})$的部分图象如图所示,点A,B是图象的最高点,点C是图象的最低点,且△ABC是正三角形,则f(1)+f(2)+f(3)的值为( )
函数$f(x)=3\sqrt{3}sinωx({ω>0})$的部分图象如图所示,点A,B是图象的最高点,点C是图象的最低点,且△ABC是正三角形,则f(1)+f(2)+f(3)的值为( )
 函数$f(x)=3\sqrt{3}sinωx({ω>0})$的部分图象如图所示,点A,B是图象的最高点,点C是图象的最低点,且△ABC是正三角形,则f(1)+f(2)+f(3)的值为( )
函数$f(x)=3\sqrt{3}sinωx({ω>0})$的部分图象如图所示,点A,B是图象的最高点,点C是图象的最低点,且△ABC是正三角形,则f(1)+f(2)+f(3)的值为( )| A. | $\frac{9}{2}$ | B. | $\frac{{9\sqrt{3}}}{2}$ | C. | $9\sqrt{3}+1$ | D. | $\frac{{9({\sqrt{3}+1})}}{2}$ |
5.某市对贫困家庭自主创业给予小额贷款补贴,每户贷款为2万元,贷款期限有6个月、12个月、18个月、24个月、36个月五种,这五种贷款期限政府分别需要补助200元、300元、300元、400元,从2016年享受此项政策的困难户中抽取了100户进行了调查,选取贷款期限的频数如表:
以上表各种贷款期限频率作为2017年贫困家庭选择各种贷款期限的概率.
(1)某小区2017年共有3户准备享受此项政策,计算其中恰有两户选择贷款期限为12个月的概率;
(2)设给享受此项政策的某困难户补贴为ξ元,写出ξ的分布列,若预计2017年全市有3.6万户享受此项政策,估计2017年该市共需要补贴多少万元.
| 贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
| 频数 | 20 | 40 | 20 | 10 | 10 |
(1)某小区2017年共有3户准备享受此项政策,计算其中恰有两户选择贷款期限为12个月的概率;
(2)设给享受此项政策的某困难户补贴为ξ元,写出ξ的分布列,若预计2017年全市有3.6万户享受此项政策,估计2017年该市共需要补贴多少万元.
3.已知定义在R上的函数y=f(x)满足:①对于任意的x∈R,都有f(x+2)=f(x-2);②函数y=f(x+2)是偶函数;③当x∈(0,2]时,f(x)=ex-$\frac{1}{x}$,a=f(-5),b=f($\frac{19}{2}$).c=f($\frac{41}{4}$),则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<a<b | C. | c<a<b | D. | b<a<c |
2.在区间[0,2]上随机取两个数x,y,则xy∈[0,2]的概率是( )
| A. | $\frac{1-ln2}{2}$ | B. | $\frac{3-2ln2}{4}$ | C. | $\frac{1+ln2}{2}$ | D. | $\frac{1+2ln2}{2}$ |
1.在2013年至2016年期间,甲每年6月1日都到银行存入m元的一年定期储蓄,若年利率为q保持不变,且每年到期的存款本息自动转为新的一年定期,到2017年6月1日甲去银行不再存款,而是将所有存款的本息全部取回,则取回的金额是( )
| A. | m(1+q)4元 | B. | m(1+q)5元 | C. | $\frac{m[(1+q)^{4}-(1+q)]}{q}$元 | D. | $\frac{m[(1+q)^{5}-(1+q)]}{q}$元 |
20.已知a、b∈{2,3,4,5,6,7,8,9},则logab的不同取值个数为( )
| A. | 53 | B. | 56 | C. | 55 | D. | 57 |
19.已知直线l:kx-y-3=0与圆O:x2+y2=4交于A、B两点且$\overrightarrow{OA}$•$\overrightarrow{OB}$=2,则k=( )
| A. | 2 | B. | ±$\sqrt{2}$ | C. | ±2 | D. | $\sqrt{2}$ |
17.设复数z=$\frac{1+2i}{(1-i)^{2}}$,则z的虚部是( )
0 239670 239678 239684 239688 239694 239696 239700 239706 239708 239714 239720 239724 239726 239730 239736 239738 239744 239748 239750 239754 239756 239760 239762 239764 239765 239766 239768 239769 239770 239772 239774 239778 239780 239784 239786 239790 239796 239798 239804 239808 239810 239814 239820 239826 239828 239834 239838 239840 239846 239850 239856 239864 266669
| A. | $\frac{1}{2}$i | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{1}{2}$i |