题目内容
4.在等差数列{an}中,a1=2017,其前n项和为Sn,若$\frac{{S}_{2013}}{2013}$-$\frac{{S}_{2011}}{2011}$=2,则S2017=2017.分析 根据等差数列的前n项和公式,求出数列的公差即可.
解答 解:在等差数列中$\frac{{S}_{n}}{n}$=$\frac{n{a}_{1}+\frac{n(n-1)d}{2}}{n}$=a1+$\frac{n-1}{2}$d=$\frac{d}{2}$n+a1-$\frac{d}{2}$为等差数列,
则由$\frac{{S}_{2013}}{2013}$-$\frac{{S}_{2011}}{2011}$=2得$\frac{d}{2}$×2013-$\frac{d}{2}$×2011=d=2,
则S2017=2017×2017-$\frac{2017×2016}{2}×2$=2017(2017-2016)=2017,
故答案为:2017
点评 本题主要考查等差数列前n项和公式的应用,根据条件建立方程关系求出公差是解决本题的关键.

练习册系列答案
相关题目
14.一个几何体的三视图如图所示,则它的体积为( )


| A. | $\frac{20}{3}$ | B. | $\frac{40}{3}$ | C. | $\frac{8}{3}$ | D. | 40 |
19.已知直线l:kx-y-3=0与圆O:x2+y2=4交于A、B两点且$\overrightarrow{OA}$•$\overrightarrow{OB}$=2,则k=( )
| A. | 2 | B. | ±$\sqrt{2}$ | C. | ±2 | D. | $\sqrt{2}$ |
14.同时掷两个骰子,各掷一次,向上的点数之和是6的概率是( )
| A. | $\frac{1}{12}$ | B. | $\frac{5}{36}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{6}$ |
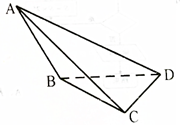 如图所示,在三棱锥A-BCD中,侧面ABD,ACD是全等的直角三角形,AD是公共的斜边且AD=$\sqrt{3}$,BD=CD=1,另一侧面ABC是正三角形.
如图所示,在三棱锥A-BCD中,侧面ABD,ACD是全等的直角三角形,AD是公共的斜边且AD=$\sqrt{3}$,BD=CD=1,另一侧面ABC是正三角形.