题目内容
20.已知a、b∈{2,3,4,5,6,7,8,9},则logab的不同取值个数为( )| A. | 53 | B. | 56 | C. | 55 | D. | 57 |
分析 根据题意,由乘法原理可得a、b的取法都有8种,即logab的可能情况有8×8=64种,由对数的性质分析其中重复的情况,在全部数目中将重复的排除即可得答案.
解答 解:根据题意,a、b∈{2,3,4,5,6,7,8,9},
则a、b的取法都有8种,即logab的可能情况有8×8=64种,
其中当a=b时,logab=1,有8种情况是重复的,
log24=log39=2,有2种情况是重复的,
log32=log94,有2种情况是重复的,
log42=log93=$\frac{1}{2}$,有2种情况是重复的,
log23=log49,有2种情况是重复的,
则logab的不同取值有64-7-1-1-1-1=53种;
故选:A.
点评 本题考查排列组合的应用,涉及对数的运算,注意其中对数值相等,即取值重复的情况.

练习册系列答案
相关题目
11.把函数f(x)=cos2($\frac{π}{2}$x-$\frac{π}{6}$)的图象向左平移$\frac{1}{3}$个单位后得到的函数为g(x),则以下结论中正确的是( )
| A. | g($\frac{1}{5}$)>g($\frac{8}{5}$)>0 | B. | g($\frac{1}{5}$)$>0>g(\frac{8}{5})$ | C. | g($\frac{8}{5}$)>g($\frac{1}{5}$)>0 | D. | g($\frac{1}{5}$)=g($\frac{8}{5}$)>0 |
15.已知命题$p:?x>e,{({\frac{1}{2}})^x}$>lnx;命题q:?a>1,b>1,logab+2logba≥2$\sqrt{2}$,则下列命题中为真命题的是( )
| A. | (?p)∧q | B. | p∧q | C. | p∧(?q) | D. | p∨(?q) |
5.某市对贫困家庭自主创业给予小额贷款补贴,每户贷款为2万元,贷款期限有6个月、12个月、18个月、24个月、36个月五种,这五种贷款期限政府分别需要补助200元、300元、300元、400元,从2016年享受此项政策的困难户中抽取了100户进行了调查,选取贷款期限的频数如表:
以上表各种贷款期限频率作为2017年贫困家庭选择各种贷款期限的概率.
(1)某小区2017年共有3户准备享受此项政策,计算其中恰有两户选择贷款期限为12个月的概率;
(2)设给享受此项政策的某困难户补贴为ξ元,写出ξ的分布列,若预计2017年全市有3.6万户享受此项政策,估计2017年该市共需要补贴多少万元.
| 贷款期限 | 6个月 | 12个月 | 18个月 | 24个月 | 36个月 |
| 频数 | 20 | 40 | 20 | 10 | 10 |
(1)某小区2017年共有3户准备享受此项政策,计算其中恰有两户选择贷款期限为12个月的概率;
(2)设给享受此项政策的某困难户补贴为ξ元,写出ξ的分布列,若预计2017年全市有3.6万户享受此项政策,估计2017年该市共需要补贴多少万元.
9.已知函数f(x)=x2+bx过(1,3)点,若数列{$\frac{1}{f(n)}$}的前n项和为Sn,则Sn的值为( )
| A. | $\frac{n+1}{n+2}$ | B. | $\frac{n+1}{2n+4}$ | C. | $\frac{3}{2}$-$\frac{2n+3}{(n+1)(n+2)}$ | D. | $\frac{3}{4}$-$\frac{2n+3}{2(n+1)(n+2)}$ |
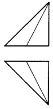
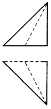
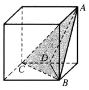 如图是一个正方体,A,B,C为三个顶点,D是棱的中点,则三棱锥A-BCD的正视图,俯视图是(注:选项中的上图是正视图,下图是俯视图)( )
如图是一个正方体,A,B,C为三个顶点,D是棱的中点,则三棱锥A-BCD的正视图,俯视图是(注:选项中的上图是正视图,下图是俯视图)( )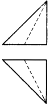
 如图,在四棱锥P-ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2
如图,在四棱锥P-ABCD中,AB⊥平面BCP,CD∥平面ABP,AB=BC=CP=BP=2CD=2