题目内容
18.下列命题中正确命题的个数是( )(1)对于命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,均有x2+x+1>0;
(2)命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题;
(3)回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为$\widehat{y}$=1.23x+0.08;
(4)m=3是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件.
| A. | 1 | B. | 3 | C. | 2 | D. | 4 |
分析 直接写出特称命题的否定判断(1);写出原命题的逆否命题并判断真假判断(2);由已知结合回归直线方程恒过样本中心点求得a,得到回归直线方程判断(3);由两直线垂直与系数的关系列式求出m值判断(4).
解答 解:(1)命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R,均有x2+x+1≥0,故(1)错误;
(2)命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”的逆否命题为:“已知x,y∈R,若x=2且y=1,则x+y=3”是真命题,
∴命题“已知x,y∈R,若x+y≠3,则x≠2或y≠1”是真命题,故(2)正确;
(3)设回归直线方程为$\widehat{y}$=1.23x+a,把样本点的中心(4,5)代入,得a=5-1.23×4=0.08,则回归直线方程为$\widehat{y}$=1.23x+0.08,故(3)正确;
(4)由m(m+3)-6m=0,得m=0或m=3,∴m=3是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充分不必要条件,故(4)错误.
∴正确命题的个数是2.
故选:C.
点评 本题考查命题的真假判断与应用,考查命题的否定与逆否命题,考查充分必要条件的判定方法,是中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
8.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )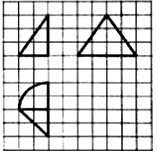

| A. | 2+π | B. | 2+4π | C. | 6+π | D. | 6+4π |
9.设复数z满足z(1+i)=4,则|$\overline{z}$|等于( )
| A. | 2$\sqrt{2}$ | B. | 8 | C. | 2-2i | D. | 2+2i |
3.已知定义在R上的函数y=f(x)满足:①对于任意的x∈R,都有f(x+2)=f(x-2);②函数y=f(x+2)是偶函数;③当x∈(0,2]时,f(x)=ex-$\frac{1}{x}$,a=f(-5),b=f($\frac{19}{2}$).c=f($\frac{41}{4}$),则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<a<b | C. | c<a<b | D. | b<a<c |
7.设命题p:?x∈R,ex≥x+1,则¬p为( )
| A. | ?x∈R,ex<x+1 | B. | ?x0∈R,ex0<x0+1 | C. | ?x0∈R,ex0≤x0+1 | D. | ?x∈R,ex0≥x0+1 |