19.已知$cos({\frac{π}{4}-α})=\frac{4}{5}$,则sin2α=( )
| A. | $\frac{24}{25}$ | B. | $\frac{7}{25}$ | C. | $±\frac{24}{25}$ | D. | $±\frac{7}{25}$ |
18.已知平面向量$\vec a=({1,2}),\vec b=({-2,m})$,且$\vec a∥\vec b$,则$|{\vec b}|$为( )
| A. | 2$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | 3$\sqrt{5}$ | D. | 1 |
15.同时具有性质:“①最小正周期是π;②图象关于直线$x=\frac{π}{3}$对称;③在$[{-\frac{π}{6},\frac{π}{3}}]$上是增函数.”的一个函数为( )
| A. | $y=sin({\frac{x}{2}+\frac{π}{6}})$ | B. | $y=cos({\frac{x}{2}-\frac{π}{6}})$ | C. | $y=cos({2x+\frac{π}{6}})$ | D. | $y=sin({2x-\frac{π}{6}})$ |
10.“共享单车”的出现,为我们提供了一种新型的交通方式.某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:
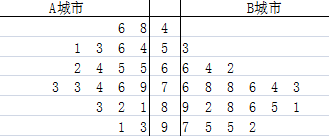
(Ⅰ)根据茎叶图,比较两城市满意度评分的平均值和方差(不要求计算出具体值,得出结论即可);
(Ⅱ)若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成下列2×2列联表,并据此样本分析你是否有95%的把握认为城市拥堵与认可共享单车有关.
(参考公式:${Χ^2}=\frac{{n{{({n_{11}}{n_{22}}-{n_{12}}{n_{21}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$)
(Ⅲ)在A和B两个城市满意度在90分以上的用户中任取2户,求来自不同城市的概率.
0 239194 239202 239208 239212 239218 239220 239224 239230 239232 239238 239244 239248 239250 239254 239260 239262 239268 239272 239274 239278 239280 239284 239286 239288 239289 239290 239292 239293 239294 239296 239298 239302 239304 239308 239310 239314 239320 239322 239328 239332 239334 239338 239344 239350 239352 239358 239362 239364 239370 239374 239380 239388 266669

(Ⅰ)根据茎叶图,比较两城市满意度评分的平均值和方差(不要求计算出具体值,得出结论即可);
(Ⅱ)若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成下列2×2列联表,并据此样本分析你是否有95%的把握认为城市拥堵与认可共享单车有关.
| 认可 | 不认可 | 合计 | |
| A城市 | |||
| B城市 | |||
| 合计 |
| P(Χ2≥k) | 0.05 | 0.010 |
| k | 3.841 | 6.635 |
(Ⅲ)在A和B两个城市满意度在90分以上的用户中任取2户,求来自不同城市的概率.

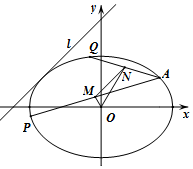 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率$e=\frac{{\sqrt{2}}}{2}$,且与直线l:y=x+3相切.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率$e=\frac{{\sqrt{2}}}{2}$,且与直线l:y=x+3相切.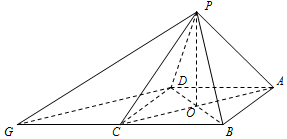 在四棱锥P-ABCD中,底面ABCD为菱形,∠PAD=∠PAB,AC交BD于O,
在四棱锥P-ABCD中,底面ABCD为菱形,∠PAD=∠PAB,AC交BD于O,