题目内容
15.同时具有性质:“①最小正周期是π;②图象关于直线$x=\frac{π}{3}$对称;③在$[{-\frac{π}{6},\frac{π}{3}}]$上是增函数.”的一个函数为( )| A. | $y=sin({\frac{x}{2}+\frac{π}{6}})$ | B. | $y=cos({\frac{x}{2}-\frac{π}{6}})$ | C. | $y=cos({2x+\frac{π}{6}})$ | D. | $y=sin({2x-\frac{π}{6}})$ |
分析 利用正弦函数的图象和性质,逐一判断各个选项是否正确,从而得出结论.
解答 解:由于y=sin($\frac{x}{2}$+$\frac{π}{6}$)的最小正周期为$\frac{2π}{\frac{1}{2}}$=4π,不满足①,故排除A.
由于y=cos($\frac{x}{2}$-$\frac{π}{6}$)的最小正周期为$\frac{2π}{\frac{1}{2}}$=4π,不满足①,故排除B.
由于y=cos(2x+$\frac{π}{6}$),在$[{-\frac{π}{6},\frac{π}{3}}]$上,2x+$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],
故y=cos(2x+$\frac{π}{6}$)在$[{-\frac{π}{6},\frac{π}{3}}]$上没有单调性,故排除C.
对于y=sin(2x-$\frac{π}{6}$)的最小正周期为$\frac{2π}{2}$=π;
当$x=\frac{π}{3}$时,函数取得最大值为1,故图象关于直线$x=\frac{π}{3}$对称;
在$[{-\frac{π}{6},\frac{π}{3}}]$上,2x-$\frac{π}{6}$∈[-$\frac{π}{2}$,$\frac{π}{2}$],故y=sin(2x-$\frac{π}{6}$)在$[{-\frac{π}{6},\frac{π}{3}}]$上是增函数,
故D满足题中的三个条件,
故选:D.
点评 本题主要考查正弦函数的图象和性质,属于中档题.

练习册系列答案
相关题目
5.如果x0是函数f(x)的一个零点,且在这个零点两侧函数值异号,则称x0是函数f(x)的一个变号零点,已知函数f(x)=ax2+1+lnx在($\frac{1}{e}$,e)上有且仅有一个变号零点,则实数a的取值范围为( )
| A. | [-$\frac{2}{{e}^{2}}$,0) | B. | [-$\frac{2}{{e}^{2}}$,0)∪{$-\frac{1}{2}$e} | C. | [-$\frac{e}{2}$,0) | D. | [-$\frac{2}{{e}^{2}}$,0] |
6.已知直线$\sqrt{3}x-y-\sqrt{3}=0$与抛物线y2=4x交于A,B两点(A在x轴上方),与x轴交于F点,$\overrightarrow{OF}=λ\overrightarrow{OA}+μ\overrightarrow{OB}$,则λ-μ=( )
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
3.已知A(5,3),F是抛物线y2=4x的焦点,P是抛物线上的动点,则△PAF周长的最小值为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 15 |
10.“共享单车”的出现,为我们提供了一种新型的交通方式.某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:
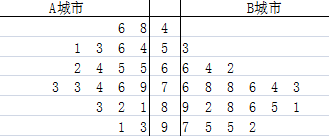
(Ⅰ)根据茎叶图,比较两城市满意度评分的平均值和方差(不要求计算出具体值,得出结论即可);
(Ⅱ)若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成下列2×2列联表,并据此样本分析你是否有95%的把握认为城市拥堵与认可共享单车有关.
(参考公式:${Χ^2}=\frac{{n{{({n_{11}}{n_{22}}-{n_{12}}{n_{21}})}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}$)
(Ⅲ)在A和B两个城市满意度在90分以上的用户中任取2户,求来自不同城市的概率.

(Ⅰ)根据茎叶图,比较两城市满意度评分的平均值和方差(不要求计算出具体值,得出结论即可);
(Ⅱ)若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成下列2×2列联表,并据此样本分析你是否有95%的把握认为城市拥堵与认可共享单车有关.
| 认可 | 不认可 | 合计 | |
| A城市 | |||
| B城市 | |||
| 合计 |
| P(Χ2≥k) | 0.05 | 0.010 |
| k | 3.841 | 6.635 |
(Ⅲ)在A和B两个城市满意度在90分以上的用户中任取2户,求来自不同城市的概率.
20.椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的中心在原点,F1,F2分别为左、右焦点,A,B分别是椭圆的上顶点和右顶点,P是椭圆上一点,且PF1⊥x轴,PF2∥AB,则此椭圆的离心率等于( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
7.已知命题p1:若sinx≠0,则sinx+$\frac{1}{sinx}$≥2恒成立;p2:x+y=0的充要条件是$\frac{x}{y}$=-1,则下列命题为真命题的是( )
| A. | p1∧p2 | B. | p1∨p2 | C. | p1∧(¬p2) | D. | (¬p1)∨p2 |
19.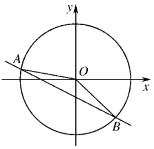 如图,直线x+2y=a与圆x2+y2=1相交于不同的两点A(x1,y1),B(x2,y2),O为坐标原点,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=a,则实数a的值为( )
如图,直线x+2y=a与圆x2+y2=1相交于不同的两点A(x1,y1),B(x2,y2),O为坐标原点,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=a,则实数a的值为( )
 如图,直线x+2y=a与圆x2+y2=1相交于不同的两点A(x1,y1),B(x2,y2),O为坐标原点,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=a,则实数a的值为( )
如图,直线x+2y=a与圆x2+y2=1相交于不同的两点A(x1,y1),B(x2,y2),O为坐标原点,若$\overrightarrow{OA}$•$\overrightarrow{OB}$=a,则实数a的值为( )| A. | $\frac{5-\sqrt{65}}{4}$ | B. | $\frac{\sqrt{65}-5}{4}$ | C. | $\frac{5-\sqrt{55}}{4}$ | D. | $\frac{\sqrt{55}-5}{4}$ |