��Ŀ����
10���������������ij��֣�Ϊ�����ṩ��һ�����͵Ľ�ͨ��ʽ��ij����Ϊ�˵������ǶԴ��ֽ�ͨ��ʽ������ȣ��ӽ�ͨӵ�²����ص�A���кͽ�ͨӵ�����ص�B���зֱ����������20���û����õ���һ���û���������ֵ������������Ƴ���Ҷͼ��ͼ��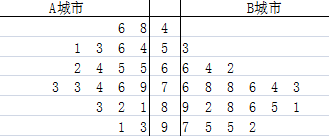
�����ݾ�Ҷͼ���Ƚ���������������ֵ�ƽ��ֵ�ͷ����Ҫ����������ֵ���ó����ۼ��ɣ���
�������÷ֲ�����80�֣�����Ϊ���û��Դ��ֽ�ͨ��ʽ���Ͽɡ���������Ϊ���û��Դ��ֽ�ͨ��ʽ�����Ͽɡ�������ݴ������������2��2�����������ݴ������������Ƿ���95%�İ�����Ϊ����ӵ�����Ͽɹ��������йأ�
| �Ͽ� | ���Ͽ� | �ϼ� | |
| A���� | |||
| B���� | |||
| �ϼ� |
| P����2��k�� | 0.05 | 0.010 |
| k | 3.841 | 6.635 |
������A��B���������������90�����ϵ��û�����ȡ2���������Բ�ͬ���еĸ��ʣ�
���� �����ݾ�Ҷͼ�����ɱȽ���������������ֵ�ƽ��ֵ�ͷ��
���������2�����ٽ�ֵ�Ƚϣ����ɵó����ۣ�
���������оٷ�ȷ�������¼�������������Բ�ͬ���еĸ��ʣ���
��� �⣺����A�������ֵ�ƽ��ֵС��B�������ֵ�ƽ��ֵ�� ��2�֣�
A�������ֵķ������B�������ֵķ�� ��4�֣�
����2��2������
| �Ͽ� | ���Ͽ� | �ϼ� | |
| A���� | 5 | 15 | 20 |
| B���� | 10 | 10 | 20 |
| �ϼ� | 15 | 25 | 40 |
������Ϊ��95%�İ�����Ϊ����ӵ�����Ͽɹ��������� ��8�֣�
���� ���¼�M=�����Բ�ͬ���С�����A���е�2����Ϊa��b��B���е�4����Ϊc��d��e��f�����д�����ȡ2���Ļ����¼��ֱ�Ϊ��a��b������a��c������a��d������a��e������a��f������b��c������b��d������b��e������b��f������c��d������c��e������c��f������d��e������d��f������e��f������15�� ��10�֣�
�����¼�M�����Բ�ͬ���С������Ļ����¼�Ϊ����a��c������a��d������a��e������a��f������b��c������b��d������b��e������b��f����8�֣������¼�M�����Բ�ͬ���С��ĸ�����$p��M��=\frac{8}{15}$����12�֣�
���� ������Ҫ�������ͳ�Ƶ����֪ʶ�����龥Ҷͼ�������Լ���֪ʶ�����ã�������ʵļ��㣬�����е��⣮

��ϰ��ϵ�д�
�����Ŀ
20����֪˫����$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1��a��0��b��0�������Ҷ���ֱ�ΪA1��A2��M��˫����������A1��A2������һ�㣬ֱ��MA1��MA2�ֱ���y�ύ��P��Q���㣬OΪ����ԭ�㣬��|OP|��|OM|��|OQ|���γɵȱ����У���˫���ߵ������ʵ�ȡֵ��Χ�ǣ�������
| A�� | $��{\sqrt{2}��+��}��$ | B�� | $[{\sqrt{2}��+��}��$ | C�� | $��{1��\sqrt{2}}��$ | D�� | $��{1��\sqrt{2}}]$ |
1���躯��f��x��=��x-2��n������$n=4\int_{-��}^{2��}{sin��{x+��}��dx}$����f��x����չ��ʽ�к�x6�����ϵ��Ϊ��������
| A�� | -112 | B�� | -56 | C�� | 112 | D�� | 56 |
18��������A={x|1��x��2}��B={x|x2-3x+2=0}����A��B���ڣ�������
| A�� | {x|1��x��2} | B�� | ��1��2�� | C�� | {1��2} | D�� | ∅ |
5����֪����{an}�ǵȲ�����������a1=1��a3=7����SnΪ����{��-1��nan}��ǰn��ͣ���S2017Ϊ��������
| A�� | -3025 | B�� | -3024 | C�� | 2017 | D�� | 9703 |
15��ͬʱ�������ʣ�������С�������ǦУ���ͼ�����ֱ��$x=\frac{��}{3}$�Գƣ�����$[{-\frac{��}{6}��\frac{��}{3}}]$����������������һ������Ϊ��������
| A�� | $y=sin��{\frac{x}{2}+\frac{��}{6}}��$ | B�� | $y=cos��{\frac{x}{2}-\frac{��}{6}}��$ | C�� | $y=cos��{2x+\frac{��}{6}}��$ | D�� | $y=sin��{2x-\frac{��}{6}}��$ |
2����֪����M={x|y=$\sqrt{1-3x}$}������N={x|x2-1��0}����M��N=��������
| A�� | {x|-1��x��$\frac{1}{3}$} | B�� | {x|x��$\frac{1}{3}$} | C�� | {x|x��$\frac{1}{3}$} | D�� | {x|$\frac{1}{3}$��x��1} |
19��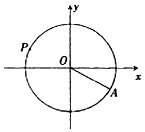 ˮ���ڹŴ��ǽ��й����ˮ�Ĺ��ߣ��������һ����ϵķ�����Ҳ������������Ȼ������Ȼ����������ͼ��һ���뾶ΪR��ˮ����һ��ˮ���ӵ�A��3$\sqrt{3}$��-3����������Բ�ܰ���ʱ�뷽��������ת������תһ����ʱ60�룮����t���ˮ����ת��P�㣬��P������Ϊ��x��y����������������y=f��t��=Rsin����t+�գ���t��0���أ�0��|��|��$\frac{��}{2}}$��������������������ǣ�������
ˮ���ڹŴ��ǽ��й����ˮ�Ĺ��ߣ��������һ����ϵķ�����Ҳ������������Ȼ������Ȼ����������ͼ��һ���뾶ΪR��ˮ����һ��ˮ���ӵ�A��3$\sqrt{3}$��-3����������Բ�ܰ���ʱ�뷽��������ת������תһ����ʱ60�룮����t���ˮ����ת��P�㣬��P������Ϊ��x��y����������������y=f��t��=Rsin����t+�գ���t��0���أ�0��|��|��$\frac{��}{2}}$��������������������ǣ�������
 ˮ���ڹŴ��ǽ��й����ˮ�Ĺ��ߣ��������һ����ϵķ�����Ҳ������������Ȼ������Ȼ����������ͼ��һ���뾶ΪR��ˮ����һ��ˮ���ӵ�A��3$\sqrt{3}$��-3����������Բ�ܰ���ʱ�뷽��������ת������תһ����ʱ60�룮����t���ˮ����ת��P�㣬��P������Ϊ��x��y����������������y=f��t��=Rsin����t+�գ���t��0���أ�0��|��|��$\frac{��}{2}}$��������������������ǣ�������
ˮ���ڹŴ��ǽ��й����ˮ�Ĺ��ߣ��������һ����ϵķ�����Ҳ������������Ȼ������Ȼ����������ͼ��һ���뾶ΪR��ˮ����һ��ˮ���ӵ�A��3$\sqrt{3}$��-3����������Բ�ܰ���ʱ�뷽��������ת������תһ����ʱ60�룮����t���ˮ����ת��P�㣬��P������Ϊ��x��y����������������y=f��t��=Rsin����t+�գ���t��0���أ�0��|��|��$\frac{��}{2}}$��������������������ǣ�������| A�� | $R=6����=\frac{��}{30}����=-\frac{��}{6}$ | |
| B�� | ��t��[35��55]ʱ����P��x��ľ�������ֵΪ6 | |
| C�� | ��t��[10��25]ʱ������y=f��t�������ݼ� | |
| D�� | ��t=20ʱ��$|{PA}|=6\sqrt{3}$ |
14���躯��f��x��=��x-a��2+��ln x2-2a��2������x��0��a��R������x0ʹ��f��x0����b��������ʵ��b����СֵΪ��������
| A�� | $\frac{1}{5}$ | B�� | $\frac{2}{5}$ | C�� | $\frac{4}{5}$ | D�� | 1 |