题目内容
16.已知随机变量X服从正态分布N(3,σ2),且P(X<5)=0.8,则P(1<X<3)=0.3.分析 根据随机变量X服从正态分布N(3,σ2),看出这组数据对应的正态曲线的对称轴x=3,根据正态曲线的特点,即可得到结果.
解答 解:∵随机变量X服从正态分布N(3,σ2),
∴对称轴是x=3.
∵P(X<5)=0.8,
∴P(X≥5)=0.2,
∴PP(1<X<3)=0.5-0.2=0.3.
故答案为0.3.
点评 本题考查正态分布曲线的特点及曲线所表示的意义,考查正态曲线的对称性,考查对称区间的概率相等,本题是一个基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知集合A={x|x2+x-2<0},B={x|y=log2x},则A∩B=( )
| A. | (-2,1) | B. | (-2,0) | C. | (0,+∞) | D. | (0,1) |
7.数列{an}的前n项和为Sn,a1=1,${a_n}+{a_{n+1}}=3×{2^{n-1}}$,则S2017=( )
| A. | 22018-1 | B. | 22018+1 | C. | 22017-1 | D. | 22017+1 |
4.将长宽分别为2和1的长方形ABCD沿对角线AC折起,得到四面体A-BCD,则四面体A-BCD外接球的表面积为( )
| A. | 3π | B. | 5π | C. | 10π | D. | 20π |
8.已知函数f(x)=sin(x+φ)-$\sqrt{3}$cos(x+φ)(|φ|<$\frac{π}{2}$)的图象关于直线x=π对称,则cos2φ=( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
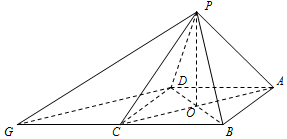 在四棱锥P-ABCD中,底面ABCD为菱形,∠PAD=∠PAB,AC交BD于O,
在四棱锥P-ABCD中,底面ABCD为菱形,∠PAD=∠PAB,AC交BD于O,