Question

12．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的离心率$e=\frac{{\sqrt{2}}}{2}$，且与直线l：y=x+3相切．
（Ⅰ）求椭圆的标准方程；
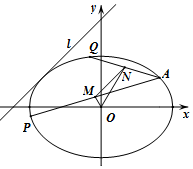
（Ⅱ）过椭圆上点A（2，1）作椭圆的弦AP，AQ，若AP，AQ的中点分别为M，N，若MN平行于l，则OM，ON斜率之和是否为定值？

Answer 1

分析 （Ⅰ）由离心率可得 a²=2b²，椭圆C与直线l相切，由$\left\{\begin{array}{l}y=x+3\\ \frac{x^2}{{2{b^2}}}+\frac{y^2}{b^2}=1\end{array}\right.$，得3x²+12x+18-2b²=0，△=144-4×3（18-2b²）=0，得b²=3，a²=6，可得椭圆方程
（Ⅱ）设点P（x₁，y₁），Q（x₂，y₂），可知PQ∥MN，所以k_PQ=k_MN=1，
设直线PQ的方程为y=x+t，代入椭圆方程并化简得：3x²+4tx+2t²-6=0
由题意可知$\left\{\begin{array}{l}{x_1}+{x_2}=-\frac{4t}{3}\\{x_1}{x_2}=\frac{{2{t^2}-6}}{3}\end{array}\right.$，利用韦达定理可计算${k_{OM}}+{k_{ON}}=\frac{{2（2{t^2}-6）+（t+3）（-4t）+12t+12}}{{3{x_1}{x_2}+6（{x_1}+{x_2}）+12}}=\frac{0}{{3{x_1}{x_2}+6（{x_1}+{x_2}）+12}}=0$．

解答 解：（Ⅰ）∵$e=\frac{{\sqrt{2}}}{2}$，∴$\frac{b^2}{a^2}=\frac{{{a^2}-{c^2}}}{a^2}=1-{e^2}=\frac{1}{2}$，
  即a²=2b²（2分）
由$\left\{\begin{array}{l}y=x+3\\ \frac{x^2}{{2{b^2}}}+\frac{y^2}{b^2}=1\end{array}\right.$，得3x²+12x+18-2b²=0，
△=144-4×3（18-2b²）=0，（4分）
得b²=3，a²=6，所以椭圆方程为$\frac{x^2}{6}+\frac{y^2}{3}=1$．（5分）
（Ⅱ）设直线PQ的方程y=x+t，联立方程组$\left\{\begin{array}{l}y=x+t\\ \frac{x^2}{6}+\frac{y^2}{3}=1\end{array}\right.$
得3x²+4tx+2t²-6=0的两根为P（x₁，y₁），Q（x₂，y₂），（7分）
由题意得$M（\frac{{{x_1}+2}}{2}，\frac{{{y_1}+1}}{2}）$，$N（\frac{{{x_2}+2}}{2}，\frac{{{y_2}+1}}{2}）$，
由题意可知PQ∥MN，所以k_PQ=k_MN=1，（8分）
${x_1}+{x_2}=-\frac{4t}{3}$，${x_1}{x_2}=\frac{{2{t^2}-6}}{3}$，
${k_{OM}}+{k_{ON}}=\frac{{{y_1}+1}}{{{x_1}+2}}+\frac{{{y_2}+1}}{{{x_2}+2}}=\frac{{{x_1}+t+1}}{{{x_1}+2}}+\frac{{{x_2}+t+1}}{{{x_2}+2}}$
=$\frac{{2{x_1}{x_2}+（t+1+2）（{x_1}+{x_2}）+4（t+1）}}{{（{x_1}+2）（{x_2}+2）}}$
=$\frac{{2\frac{{2{t^2}-6}}{3}+（t+1+2）\frac{-4t}{3}+4（t+1）}}{{（{x_1}+2）（{x_2}+2）}}=0$，
所以OM，ON斜率之和是为定值0．（12分）

点评 本题考查了椭圆的方程，椭圆与直线的位置关系，定值问题的处理方法，属于中档题．