题目内容
19.已知$cos({\frac{π}{4}-α})=\frac{4}{5}$,则sin2α=( )| A. | $\frac{24}{25}$ | B. | $\frac{7}{25}$ | C. | $±\frac{24}{25}$ | D. | $±\frac{7}{25}$ |
分析 根据余弦的和与差公式打开,采用两边平方,可得sin2α的值.
解答 解:由$cos({\frac{π}{4}-α})=\frac{4}{5}$,
可得:cos$\frac{π}{4}$cosα+sin$\frac{π}{4}$sinα=$\frac{4}{5}$,
则cosα+sinα=$\frac{4\sqrt{2}}{5}$,
两边平方,得1+sin2α=$\frac{32}{25}$,
则sin2α=$\frac{7}{25}$.
故选:B.
点评 本题主要考查函数值的计算,利用三角函数的倍角公式是解决本题的关键.

练习册系列答案
相关题目
9.将函数$f(x)=sin({2x+φ})({|φ|<\frac{π}{2}})$的图象向左平移$\frac{π}{3}$个单位长度后,所得函数g(x)的图象关于原点对称,则函数f(x)在$[{0,\frac{π}{2}}]$的最大值为( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
11.已知球O的半径为1,A,B是球面上的两点,且AB=$\sqrt{3}$,若点P是球面上任意一点,则$\overrightarrow{PA}$•$\overrightarrow{PB}$的取值范围是( )
| A. | [$-\frac{3}{2}$,$\frac{1}{2}$] | B. | [$-\frac{1}{2}$,$\frac{3}{2}$] | C. | [0,$\frac{1}{2}$] | D. | [0,$\frac{3}{2}$] |
2.函数f(x)=3x2+ex-2(x<0)与g(x)=3x2+ln(x+t)图象上存在关于y轴对称的点,则t的取值范围是( )
| A. | (-∞,$\frac{1}{e}$) | B. | (-∞,e) | C. | (-e,$\frac{1}{e}$) | D. | (-$\frac{1}{e}$,e) |
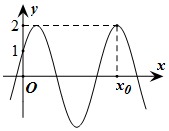 已知函数$f(x)=2sin(2x+φ)(|φ|<\frac{π}{2})$部分图象如图所示.
已知函数$f(x)=2sin(2x+φ)(|φ|<\frac{π}{2})$部分图象如图所示.