6.设函数f(x)的定义域为D,若满足条件:存在[a,b]⊆D,使f(x)在[a,b]上的值域为[$\frac{a}{2}$,$\frac{b}{2}$],则称f(x)为“倍缩函数”.若函数f(x)=lnx+t为“倍缩函数”,则实数t的取值范围是( )
| A. | (-∞,ln2-1) | B. | (-∞,ln2-1] | C. | (1-ln2,+∞) | D. | [1-ln2,+∞) |
5.已知数列{an}是等差数列且满足a1=1,a3=7,设Sn为数列{(-1)nan}的前n项和,则S2017为( )
| A. | -3025 | B. | -3024 | C. | 2017 | D. | 9703 |
4.将长宽分别为2和1的长方形ABCD沿对角线AC折起,得到四面体A-BCD,则四面体A-BCD外接球的表面积为( )
| A. | 3π | B. | 5π | C. | 10π | D. | 20π |
3.已知A(5,3),F是抛物线y2=4x的焦点,P是抛物线上的动点,则△PAF周长的最小值为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 15 |
2.在边长为2的正方形ABCD内部取一点M,则满足∠AMB为锐角的概率是( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{8}$ | C. | $1-\frac{π}{4}$ | D. | $1-\frac{π}{8}$ |
1.已知函数f(x)=sinx+cosx,g(x)=2cosx,动直线x=t与f(x)和g(x)的图象分别交于A、B两点,则|AB|的取值范围是( )
| A. | [0,1] | B. | [0,$\sqrt{2}$] | C. | [0,2] | D. | [1,$\sqrt{2}$] |
20.已知向量$\overrightarrow a$与$\overrightarrow b$不共线,$\overrightarrow{AB}=\overrightarrow a+m\overrightarrow b$,$\overrightarrow{AC}=n\overrightarrow a+\overrightarrow b$(m,n∈R),则$\overrightarrow{AB}$与$\overrightarrow{AC}$共线的条件是( )
0 239193 239201 239207 239211 239217 239219 239223 239229 239231 239237 239243 239247 239249 239253 239259 239261 239267 239271 239273 239277 239279 239283 239285 239287 239288 239289 239291 239292 239293 239295 239297 239301 239303 239307 239309 239313 239319 239321 239327 239331 239333 239337 239343 239349 239351 239357 239361 239363 239369 239373 239379 239387 266669
| A. | m+n=0 | B. | m-n=0 | C. | mn+1=0 | D. | mn-1=0 |
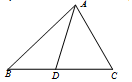 如图,已知△ABC中,D为BC上一点,∠DAC=$\frac{π}{4}$,cos∠BDA=-$\frac{3}{5}$,AC=4$\sqrt{2}$.
如图,已知△ABC中,D为BC上一点,∠DAC=$\frac{π}{4}$,cos∠BDA=-$\frac{3}{5}$,AC=4$\sqrt{2}$.