题目内容
20.已知向量$\overrightarrow a$与$\overrightarrow b$不共线,$\overrightarrow{AB}=\overrightarrow a+m\overrightarrow b$,$\overrightarrow{AC}=n\overrightarrow a+\overrightarrow b$(m,n∈R),则$\overrightarrow{AB}$与$\overrightarrow{AC}$共线的条件是( )| A. | m+n=0 | B. | m-n=0 | C. | mn+1=0 | D. | mn-1=0 |
分析 根据共线向量的共线,得到关于mn的关系即可.
解答 解:由$\overrightarrow{AB}=\overrightarrow a+m\overrightarrow b$,$\overrightarrow{AC}=n\overrightarrow a+\overrightarrow b(m,n∈R)$共线,
得$\overrightarrow a+m\overline b=λ(n\overrightarrow a+\overrightarrow b)$,即mn-1=0,
故选:D.
点评 本题考查向量共线的条件,是一道基础题.

练习册系列答案
相关题目
15.定义在R上的奇函数f(x)在(-∞,0)上递增,f(2)=1,则满足|f(log${\;}_{\frac{1}{2}}$x)|>1的x的取值范围是( )
| A. | ($\frac{1}{4}$,4) | B. | (0,$\frac{1}{2}$) | C. | (0,$\frac{1}{2}$)∪(2,+∞) | D. | (0,$\frac{1}{4}$)∪(4,+∞) |
5.已知数列{an}是等差数列且满足a1=1,a3=7,设Sn为数列{(-1)nan}的前n项和,则S2017为( )
| A. | -3025 | B. | -3024 | C. | 2017 | D. | 9703 |
9.已知中心在原点的双曲线,其右焦点与圆x2-4x+y2+1=0的圆心重合,且渐近线与该圆相离,则双曲线离心率的取值范围是( )
| A. | (1,$\frac{2\sqrt{3}}{3}$) | B. | (1,2) | C. | ($\frac{2\sqrt{3}}{3}$,+∞) | D. | (2,+∞) |
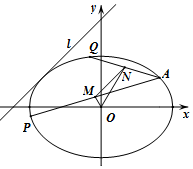 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率$e=\frac{{\sqrt{2}}}{2}$,且与直线l:y=x+3相切.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率$e=\frac{{\sqrt{2}}}{2}$,且与直线l:y=x+3相切.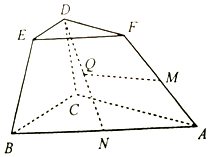 如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}({λ∈R,λ>0})$.
如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}({λ∈R,λ>0})$.