题目内容
4.将长宽分别为2和1的长方形ABCD沿对角线AC折起,得到四面体A-BCD,则四面体A-BCD外接球的表面积为( )| A. | 3π | B. | 5π | C. | 10π | D. | 20π |
分析 折叠后的四面体的外接球的半径,就是长方形ABCD沿对角线AC的一半,求出球的半径即可求出球的表面积.
解答 解:由题意可知,直角三角形斜边的中线是斜边的一半,
所以长宽分别为2和1的长方形ABCD沿对角线AC折起二面角,得到四面体A-BCD,
则四面体A-BCD的外接球的球心O为AC中点,半径$R=\frac{{\sqrt{5}}}{2}$,
所求四面体A-BCD的外接球的表面积为4π×($\frac{\sqrt{5}}{2}$)2=5π.
故选B.
点评 本题主要考查几何体的外接球的相关知识,考查空间想象能力,计算能力,求出球的半径,是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.下列函数中既是偶函数,又在区间(0,1)上单调递增的是( )
| A. | y=cosx | B. | $y={x^{\frac{1}{2}}}$ | C. | y=2|x| | D. | y=|lgx| |
19.已知i是虚数单位,则满足z-i=|1+2i|的复数z在复平面上对应点所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.已知复数z=$\frac{2i}{1+i}$,则z•$\overline z$=( )
| A. | 2 | B. | 2i | C. | 4 | D. | 4i |
8.若a,b∈R,ab≠0,且a+b=1,则下列不等式中,恒成立的是( )
| A. | a2b2≤$\frac{1}{16}$ | B. | a2+b2≥$\frac{1}{2}$ | C. | (1+$\frac{1}{a}$)(1+$\frac{1}{b}$)≥9 | D. | $\frac{1}{a}$+$\frac{1}{b}$≥4 |
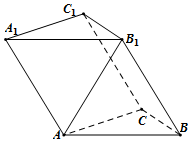 如图,在三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,△ABC和△ABB1都是边长为2的正三角形.
如图,在三棱柱ABC-A1B1C1中,侧面AA1B1B⊥底面ABC,△ABC和△ABB1都是边长为2的正三角形.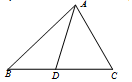 如图,已知△ABC中,D为BC上一点,∠DAC=$\frac{π}{4}$,cos∠BDA=-$\frac{3}{5}$,AC=4$\sqrt{2}$.
如图,已知△ABC中,D为BC上一点,∠DAC=$\frac{π}{4}$,cos∠BDA=-$\frac{3}{5}$,AC=4$\sqrt{2}$.