题目内容
7.已知实数x,y满足:$\left\{\begin{array}{l}{x≥1}\\{x+y≤3}\\{y≥2(x-3)}\end{array}\right.$,则z=2x+y的最小值为-2.分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数求出最小值.
解答 解:由题意得,画出约束条件所表示的可行域,如图所示,
由$\left\{\begin{array}{l}{x=1}\\{y=2(x-3)}\end{array}\right.$,解得x=2y=-4,即点A(2-4),
当目标函数z=2x+y经过点A时,取得最小值,此时最小值为
zmin=2×2+(-4)=-2.
故答案为:-2.
点评 本题考查了线性规划的相关知识与应用问题,是基础题.

练习册系列答案
相关题目
17.设等差数列{an}的前n项和为Sn,若a3+a5=4,S15=60则a20=( )
| A. | 4 | B. | 6 | C. | 10 | D. | 12 |
18.若集合M={y|y=x4,x∈(-1,0)},集合$N=\left\{{x|y=ln\frac{x}{x-1}}\right\}$,则下列各式中正确的是( )
| A. | M?N | B. | N?M | C. | M∩N=ϕ | D. | M=N |
15.定义在R上的奇函数f(x)在(-∞,0)上递增,f(2)=1,则满足|f(log${\;}_{\frac{1}{2}}$x)|>1的x的取值范围是( )
| A. | ($\frac{1}{4}$,4) | B. | (0,$\frac{1}{2}$) | C. | (0,$\frac{1}{2}$)∪(2,+∞) | D. | (0,$\frac{1}{4}$)∪(4,+∞) |
2.在边长为2的正方形ABCD内部取一点M,则满足∠AMB为锐角的概率是( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{8}$ | C. | $1-\frac{π}{4}$ | D. | $1-\frac{π}{8}$ |
19.已知$cos({\frac{π}{4}-α})=\frac{4}{5}$,则sin2α=( )
| A. | $\frac{24}{25}$ | B. | $\frac{7}{25}$ | C. | $±\frac{24}{25}$ | D. | $±\frac{7}{25}$ |
16.在(1+x)+(1+x)2+(1+x)3+…+(1+x)11的展开式中,x2的系数是( )
| A. | 55 | B. | 66 | C. | 165 | D. | 220 |
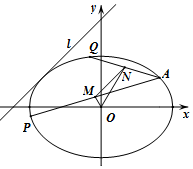 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率$e=\frac{{\sqrt{2}}}{2}$,且与直线l:y=x+3相切.
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率$e=\frac{{\sqrt{2}}}{2}$,且与直线l:y=x+3相切.