题目内容
9.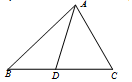 如图,已知△ABC中,D为BC上一点,∠DAC=$\frac{π}{4}$,cos∠BDA=-$\frac{3}{5}$,AC=4$\sqrt{2}$.
如图,已知△ABC中,D为BC上一点,∠DAC=$\frac{π}{4}$,cos∠BDA=-$\frac{3}{5}$,AC=4$\sqrt{2}$.( I)求AD的长;
( II)若△ABD的面积为14,求AB的长.
分析 ( I)由已知利用同角三角函数基本关系式可求$sin∠BDA=\frac{4}{5}$,利用两角差的正弦函数公式可求sinC,进而利用正弦定理即可求得AD的值.
( II)由已知及三角形面积公式可求BD的值,进而利用余弦定理可求AB的值.
解答 (本小题满分12分)
解:( I)∵$cos∠BDA=-\frac{3}{5}$,
∴$sin∠BDA=\frac{4}{5}$,…(1分)
$sinC=sin(∠BDA-\frac{π}{4})$=$sin∠BDA•cos\frac{π}{4}-cos∠BDA•sin\frac{π}{4}$=$\frac{4}{5}•\frac{{\sqrt{2}}}{2}+\frac{3}{5}•\frac{{\sqrt{2}}}{2}=\frac{{7\sqrt{2}}}{10}$,…(4分)
由正弦定理得$\frac{AC}{sin∠ADC}=\frac{AD}{sinC}$,即$\frac{{4\sqrt{2}}}{{\frac{4}{5}}}=\frac{AD}{{\frac{{7\sqrt{2}}}{10}}}$,得AD=7;…(6分)
( II)${S_{△ABD}}=\frac{1}{2}•AD•BD•sin∠ADB=\frac{1}{2}•7•BD•\frac{4}{5}=14$,得BD=5,…(8分)
由余弦定理得$A{B^2}=A{D^2}+B{D^2}-2AD•BD•cos∠ADB=49+25-2×7×5×(-\frac{3}{5})=116$,…(10分)
∴$AB=2\sqrt{29}$…(12分)
点评 本题主要考查了正、余弦定理及三角形面积公式,同角三角函数基本关系式,两角差的正弦函数公式在解三角形中的应用,考查了计算能力和转化思想,属于基础题.

 口算能手系列答案
口算能手系列答案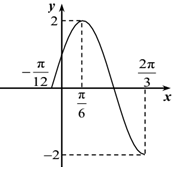 已知函数$f(x)=2sin(ωx+φ)(ω>0),x∈[{-\frac{π}{12},\frac{2π}{3}}]$的图象如图所示,若f(x1)=f(x2),且x1≠x2,则f(x1+x2)=( )
已知函数$f(x)=2sin(ωx+φ)(ω>0),x∈[{-\frac{π}{12},\frac{2π}{3}}]$的图象如图所示,若f(x1)=f(x2),且x1≠x2,则f(x1+x2)=( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
| A. | 13 | B. | 14 | C. | 15或16 | D. | 16 |
| A. | 3π | B. | 5π | C. | 10π | D. | 20π |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |