已知△ABC中,∠A,∠B,∠C的对边分别为a,b,c,若a=1且cosA=
,则△ABC的外接圆的直径等于( )
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
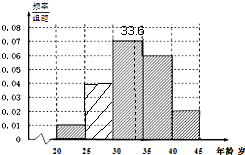 某市要对两千多名出租车司机的年龄进行调查,现从的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是( )
某市要对两千多名出租车司机的年龄进行调查,现从的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是( )| A、31.6岁 |
| B、32.6岁 |
| C、33.6岁 |
| D、36.6岁 |
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 某市要对两千多名出租车司机的年龄进行调查,现从的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是( )
某市要对两千多名出租车司机的年龄进行调查,现从的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是( )| A、31.6岁 |
| B、32.6岁 |
| C、33.6岁 |
| D、36.6岁 |