题目内容
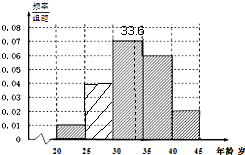某市要对两千多名出租车司机的年龄进行调查，现从的频率分布直方图如图所示，利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是（ ）| A、31.6岁 |
| B、32.6岁 |
| C、33.6岁 |
| D、36.6岁 |
考点：频率分布直方图
专题：概率与统计
分析：根据频率分布直方图的知识以及中位数的定义，估计出该市出租车司机年龄的中位数是多少．
解答：
解：设表示司机年龄在[25，30）的直方图矩形高为x，
∵5（0.01++0.07+0.06+0.02）=1，
∴=0.04；
如图，虚线表示司机年龄的中位数的估计值，其左边直方图的面积代表着50个单位，右边直方图的面积代表着50个单位，
即虚线把直方图的面积一分为二，且虚线处的数据值是33.6，
∴该市出租车司机年龄的中位数大约是33.6岁．
故选：C．
∵5（0.01++0.07+0.06+0.02）=1，
∴=0.04；
如图，虚线表示司机年龄的中位数的估计值，其左边直方图的面积代表着50个单位，右边直方图的面积代表着50个单位，
即虚线把直方图的面积一分为二，且虚线处的数据值是33.6，
∴该市出租车司机年龄的中位数大约是33.6岁．
故选：C．
点评：本题考查了用样本的数字特征估计总体的数字特征、频率分布直方图的有关知识，也考查了数形结合的思想方法，是高考常考的内容．
练习册系列答案
阳光课堂同步练习系列答案
相关题目
若z=
=x+yi，x，y∈R，则集合{x，2x，y}子集个数是（ ）
| 2-i |
| 1+2i |
| A、8 | B、7 | C、6 | D、9 |
在△ABC中，若3cos2
+5cos2
=4，则tanC的最大值为（ ）
| A-B |
| 2 |
| C |
| 2 |
A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-2
|
设变量x，y满足约束条件
，则目标函数z=3x-y的最小值为（ ）
|
| A、-8 | B、-6 | C、-4 | D、-2 |
已知双曲线C的方程是：
-
=1（m≠0），若双曲线的离心率e＞
，则实数m的取值范围是（ ）
| x2 |
| 2m-m2 |
| y2 |
| m |
| 2 |
| A、1＜m＜2． |
| B、m＜0 |
| C、m＜0或m＞1 |
| D、m＜0或1＜m＜2． |