题目内容
已知函数f(x)=ax3+bx2在点(3,f(3))处的切线方程为12x+2y-27=0.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若方程f(x)=-
x2+m有三个不同的解,求实数m的取值范围;
(Ⅲ)若不等式f(x)-
x2+(k+1)x≥0(k∈R)对于x∈(-∞,0)恒成立,求实数k的取值范围.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若方程f(x)=-
| 1 |
| 2 |
(Ⅲ)若不等式f(x)-
| 3 |
| 2 |
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)由切点在切线上,和导函数在切点处的值为切线的斜率得出方程组,求出a,b的值;
(Ⅱ)构造函数,由图象知m的值为小于极大值且大于极小值;
(Ⅲ)将不等式变形,使k在不等式一边,构造函数,恒成立,即k小于或等于函数的最小值.
(Ⅱ)构造函数,由图象知m的值为小于极大值且大于极小值;
(Ⅲ)将不等式变形,使k在不等式一边,构造函数,恒成立,即k小于或等于函数的最小值.
解答:
解:(Ⅰ)∵切点(3,f(3))在切线上,∴12×3+2f(3)-27=0,得f(3)=-
,
∴27a+9b=-
,即6a+2b=-1①,
又f′(x)=3ax2+2bx,3a×32+2b×3=-6,即9a+2b=-2 ②
由①②解得a=-
,b=
,∴函数解析式为f(x)=-
x3+
x2;
(Ⅱ)f(x)=-
x2+m,即-
x3+x2=m,
令g(x)=-
x3+x2,令g′(x)=-x2+2x>0得,0<x<2,
∴g(x)在(-∞,0)和(2,+∞)上单调递减,在(0,2)上单调递增,
∴g(x)的极小值为g(0)=0,极大值为g(2)=-
+4=
,实数m的取值范围为(0,
);
(Ⅲ)由f(x)-
x2+(k+1)x≥0(k∈R)得;k≤
x2+x-1=
(x+
)2-
,
又∵
(x+
)2-
≥-
,
∴k≤-
,即实数k的取值范围是(-∞,-
].
| 9 |
| 2 |
∴27a+9b=-
| 9 |
| 2 |
又f′(x)=3ax2+2bx,3a×32+2b×3=-6,即9a+2b=-2 ②
由①②解得a=-
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
(Ⅱ)f(x)=-
| 1 |
| 2 |
| 1 |
| 3 |
令g(x)=-
| 1 |
| 3 |
∴g(x)在(-∞,0)和(2,+∞)上单调递减,在(0,2)上单调递增,
∴g(x)的极小值为g(0)=0,极大值为g(2)=-
| 8 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
(Ⅲ)由f(x)-
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 2 |
| 7 |
| 4 |
又∵
| 1 |
| 3 |
| 3 |
| 2 |
| 7 |
| 4 |
| 7 |
| 4 |
∴k≤-
| 7 |
| 4 |
| 7 |
| 4 |
点评:本题考查了,利用导数求切线,数形结合,化归思想,解决恒成立问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
圆(x-1)2+y2=3的圆心坐标和半径分别是( )
| A、(-1,0),3 | ||
| B、(1,0),3 | ||
C、(-1,0),
| ||
D、(1,0),
|
已知向量
=(1,2),
=(2,1),则(
•
)(
-2
)等于( )
| m |
| n |
| m |
| n |
| m |
| n |
| A、(-12,0) | B、4 |
| C、(-3,0) | D、-12 |
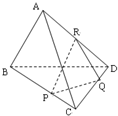 (理科)已知如图,四面体ABCD中,P,Q,R分别在棱BC,CD,DA上,且BP=2PC,CQ=2QD,DR=RA,则A,B两点到平面PQR的距离之比为( )
(理科)已知如图,四面体ABCD中,P,Q,R分别在棱BC,CD,DA上,且BP=2PC,CQ=2QD,DR=RA,则A,B两点到平面PQR的距离之比为( )| A、1:4 | B、1:3 |
| C、1:2 | D、1:1 |
已知△ABC中,∠A,∠B,∠C的对边分别为a,b,c,若a=1且cosA=
,则△ABC的外接圆的直径等于( )
| 4 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|