题目内容
下列叙述中,正确的个数是( )
①命题p:“?x∈R,x2-2≥0”的否定形式为¬p:“?x∈R,x2-2<0”;
②O是△ABC所在平面上一点,若
•
=
•
=
•
,则O是△ABC的垂心;
③“M>N”是“(
)M>(
)N”的充分不必要条件;
④命题“若x2-3x-4=0,则x=4”的逆否命题为“若x≠4,则x2-3x-4≠0”;
⑤已知
=(2,-1),
=(m,m-1),则
和
的夹角为锐角充要条件为:m>-1.
①命题p:“?x∈R,x2-2≥0”的否定形式为¬p:“?x∈R,x2-2<0”;
②O是△ABC所在平面上一点,若
| OA |
| OB |
| OB |
| OC |
| OC |
| OA |
③“M>N”是“(
| 2 |
| 3 |
| 2 |
| 3 |
④命题“若x2-3x-4=0,则x=4”的逆否命题为“若x≠4,则x2-3x-4≠0”;
⑤已知
| a |
| b |
| a |
| b |
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:直接写出命题的否定判断①;
把给出的含向量数量积的等式移项变形,得到顶点与O点的连线垂直于对边,从而说明命题②正确;
由指数函数的单调性说明③错误;
直接写出命题的逆否命题说明④正确;
举反例说明命题⑤错误.
把给出的含向量数量积的等式移项变形,得到顶点与O点的连线垂直于对边,从而说明命题②正确;
由指数函数的单调性说明③错误;
直接写出命题的逆否命题说明④正确;
举反例说明命题⑤错误.
解答:
解:对于①,命题p:“?x∈R,x2-2≥0”的否定形式为¬p:“?x∈R,x2-2<0”,
∴命题①正确;
对于②,O是△ABC所在平面上一点,由
•
=
•
,得
•(
-
)=0,即
•
=0,
∴OB⊥CA.
由
•
=
•
,得
•(
-
)=0,即
•
=0,
∴OC⊥AB.
则O为△ABC的垂心.命题②正确;
对于③,∵y=(
)x是实数集内的减函数,
∴“M>N”是“(
)M<(
)N”的充分不必要条件.命题③错误;
对于④,命题“若x2-3x-4=0,则x=4”的逆否命题为“若x≠4,则x2-3x-4≠0”.
∴命题④正确;
对于⑤,当m=
>-1时,
=(
,-
),
=(2,-1)=3(
,-
)=3
,
则
和
的夹角为0°.
∴命题⑤错误.
故正确的命题是①②④共3个.
故选:C.
∴命题①正确;
对于②,O是△ABC所在平面上一点,由
| OA |
| OB |
| OB |
| OC |
| OB |
| OA |
| OC |
| OB |
| CA |
∴OB⊥CA.
由
| OB |
| OC |
| OC |
| OA |
| OC |
| OB |
| OA |
| OC |
| AB |
∴OC⊥AB.
则O为△ABC的垂心.命题②正确;
对于③,∵y=(
| 2 |
| 3 |
∴“M>N”是“(
| 2 |
| 3 |
| 2 |
| 3 |
对于④,命题“若x2-3x-4=0,则x=4”的逆否命题为“若x≠4,则x2-3x-4≠0”.
∴命题④正确;
对于⑤,当m=
| 2 |
| 3 |
| b |
| 2 |
| 3 |
| 1 |
| 3 |
| a |
| 2 |
| 3 |
| 1 |
| 3 |
| b |
则
| a |
| b |
∴命题⑤错误.
故正确的命题是①②④共3个.
故选:C.
点评:本题考查了命题的真假判断与应用,解答②的关键是移项变形,由向量垂直得到线线垂直,通过举反例说明命题⑤起到事半功倍的效果,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知sinα+cosα=
,则sin2(
-α)=( )
| 1 |
| 3 |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
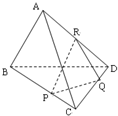 (理科)已知如图,四面体ABCD中,P,Q,R分别在棱BC,CD,DA上,且BP=2PC,CQ=2QD,DR=RA,则A,B两点到平面PQR的距离之比为( )
(理科)已知如图,四面体ABCD中,P,Q,R分别在棱BC,CD,DA上,且BP=2PC,CQ=2QD,DR=RA,则A,B两点到平面PQR的距离之比为( )| A、1:4 | B、1:3 |
| C、1:2 | D、1:1 |
 已知向量
已知向量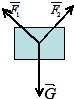 甲、乙两位同学参加2014年的自主招生考试,下火车后两人共同提起一个行李包(如图所示).设他们所用的力分别为
甲、乙两位同学参加2014年的自主招生考试,下火车后两人共同提起一个行李包(如图所示).设他们所用的力分别为