题目内容
已知函数f(x)=x+
+lnx,(a∈R).
(Ⅰ)若f(x)有最值,求实数a的取值范围;
(Ⅱ)当a≥2时,若存在x1、x2(x1≠x2),使得曲线y=f(x)在x=x1与x=x2处的切线互相平行,求证:x1+x2>8.
| a |
| x |
(Ⅰ)若f(x)有最值,求实数a的取值范围;
(Ⅱ)当a≥2时,若存在x1、x2(x1≠x2),使得曲线y=f(x)在x=x1与x=x2处的切线互相平行,求证:x1+x2>8.
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用,不等式的解法及应用
分析:(Ⅰ)求出原函数的导函数,通分整理后得到f′(x)=
,然后根据二次三项式x2+x-a对应方程根的情况分析导函数的符号,从而得到原函数的单调性,利用原函数的单调性求得使f(x)有最值的实数a的取值范围;
(Ⅱ)由曲线y=f(x)在x=x1与x=x2处的导数相等得到a=
,由已知a≥2得到2(x1+x2)≤x1•x2,
结合不等式x1•x2<(
)2可证得答案.
| x2+x-a |
| x2 |
(Ⅱ)由曲线y=f(x)在x=x1与x=x2处的导数相等得到a=
| x1x2 |
| x1+x2 |
结合不等式x1•x2<(
| x1+x2 |
| 2 |
解答:
(Ⅰ)解:∵f(x)=x+
+lnx,(a∈R),
∴f′(x)=1-
+
=
,x∈(0,+∞).
由x2+x-a对应的方程的△=1+4a知,
①当a≤-
时,f′(x)≥0,f(x)在(0,+∞)上递增,无最值;
②当-
<a≤0时,x2+x-a=0的两根均非正,
因此,f(x)在(0,+∞)上递增,无最值;
③当a>0时,x2+x-a=0有一正根x=
,
当x∈(0,
)时,f′(x)<0,f(x)在(0,
)上递减,
当x∈(
,+∞)时,f′(x)>0,f(x)在(
,+∞)上递增.
此时f(x)有最小值.
∴实数a的范围为a>0;
(Ⅱ)证明:依题意:1-
+
=1-
+
,
整理得:a(
+
)=1,
由于x1>0,x2>0,且x1≠x2,则有
a=
≥2,
∴2(x1+x2)≤x1•x2<(
)2
∴2(x1+x2)<(
)2,
则x1+x2>8.
| a |
| x |
∴f′(x)=1-
| a |
| x2 |
| 1 |
| x |
| x2+x-a |
| x2 |
由x2+x-a对应的方程的△=1+4a知,
①当a≤-
| 1 |
| 4 |
②当-
| 1 |
| 4 |
因此,f(x)在(0,+∞)上递增,无最值;
③当a>0时,x2+x-a=0有一正根x=
-1+
| ||
| 2 |
当x∈(0,
-1+
| ||
| 2 |
-1+
| ||
| 2 |
当x∈(
-1+
| ||
| 2 |
-1+
| ||
| 2 |
此时f(x)有最小值.
∴实数a的范围为a>0;
(Ⅱ)证明:依题意:1-
| a |
| x12 |
| 1 |
| x1 |
| a |
| x22 |
| 1 |
| x2 |
整理得:a(
| 1 |
| x1 |
| 1 |
| x2 |
由于x1>0,x2>0,且x1≠x2,则有
a=
| x1•x2 |
| x1+x2 |
∴2(x1+x2)≤x1•x2<(
| x1+x2 |
| 2 |
∴2(x1+x2)<(
| x1+x2 |
| 2 |
则x1+x2>8.
点评:本题考查了利用导数研究曲线上某点的切线方程,考查了利用导数研究函数的单调性,训练了利用基本不等式求最值,是中档题.

练习册系列答案
相关题目
以双曲线x2-y2=2的右焦点为圆心,且与其渐近线相切的圆的方程是( )
| A、x2+y2-4x-2=0 |
| B、x2+y2-4x+2=0 |
| C、x2+y2+4x-2=0 |
| D、x2+y2+4x+2=0 |
已知直线
x+y+m=0与圆x2+y2=9交于A,B两点,则与向量
+
(O为坐标原点)共线的一个向量为( )
| 3 |
| OA |
| OB |
A、(1,-
| ||||
B、(1,
| ||||
C、(1,
| ||||
D、(1,-
|
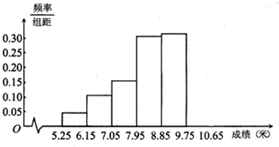 把参加某次铅球投掷的同学的成绩(单位:米)进行整理,分成以下6个小组:[5.25,6.25),[6.15,7.05),[7.05,7.95),[7.95,8.85),[8.85,9.75),[9.75,10.65),并绘制出频率分布直方图,如图所示的是这个频率分布直方图的一部分.已知从左到右前5个小组的频率分别为0.04、0.10、0.14、0.28、0.30,第6小组的频数是7.规定:投掷成绩不小于7.95米的为合格.
把参加某次铅球投掷的同学的成绩(单位:米)进行整理,分成以下6个小组:[5.25,6.25),[6.15,7.05),[7.05,7.95),[7.95,8.85),[8.85,9.75),[9.75,10.65),并绘制出频率分布直方图,如图所示的是这个频率分布直方图的一部分.已知从左到右前5个小组的频率分别为0.04、0.10、0.14、0.28、0.30,第6小组的频数是7.规定:投掷成绩不小于7.95米的为合格.