题目内容
已知O为坐标原点，对于函数f（x）=asinx+bcosx，称向量
=（a，b）为函数f（x）的伴随向量，同时称函数f（x）为向量
的伴随函数．
（Ⅰ）设函数g（x）=sin（
+x）+2cos（
-x），试求g（x）的伴随向量
的模；
（Ⅱ）记
=（1，
）的伴随函数为h（x），求使得关于x的方程h（x）-t=0在[0，
]内恒有两个不相等实数解的实数的取值范围．
| OM |
| OM |
（Ⅰ）设函数g（x）=sin（
| π |
| 2 |
| π |
| 2 |
| OM |
（Ⅱ）记
| ON |
| 3 |
| π |
| 2 |
考点：函数y=Asin（ωx+φ）的图象变换,三角函数中的恒等变换应用
专题：三角函数的图像与性质,平面向量及应用
分析：（Ⅰ）利用三角函数的诱导公式化简函数g（x），结合已知的新定义求得伴随向量
的坐标，再由模的计算公式求模；
（Ⅱ）根据给出的
=（1，
），求得其伴随函数h（x），由给出的x的范围求得h（x）的值域，再结合函数的单调性求使得关于x的方程h（x）-t=0在[0，
]内恒有两个不相等实数解的实数t的取值范围．
| OM |
（Ⅱ）根据给出的
| ON |
| 3 |
| π |
| 2 |
解答：
解：（Ⅰ）∵g(x)=sin(
+x)+2cos(
-x)=2sinx+cosx，
∴
=(2，1)．
故|
|=
=
；
（Ⅱ）∵
=（1，
），
∴
=（1，
）的伴随函数h(x)=sinx+
cosx=2sin(x+
)，
∵0≤x≤
，
∴
≤x+
≤
，
故h（x）∈[1，2]．
∵当x∈[0，
]时，函数h（x）单调递增，且h(x)∈[
，2]；
当x∈(
，
]时，函数h（x）单调递减，且h（x）∈[1，2）．
∴使得关于x的方程h（x）-t=0在[0，
]内恒有两个不相等实数解的实数的取值范围为t∈[
，2)．
| π |
| 2 |
| π |
| 2 |
∴
| OM |
故|
| OM |
| 22+12 |
| 5 |
（Ⅱ）∵
| ON |
| 3 |
∴
| ON |
| 3 |
| 3 |
| π |
| 3 |
∵0≤x≤
| π |
| 2 |
∴
| π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
故h（x）∈[1，2]．
∵当x∈[0，
| π |
| 6 |
| 3 |
当x∈(
| π |
| 6 |
| π |
| 2 |
∴使得关于x的方程h（x）-t=0在[0，
| π |
| 2 |
| 3 |
点评：本题考查了三角函数的图象和性质，考查了三角函数的诱导公式，训练了利用三角函数的单调性求函数的值域，体现了数形结合的解题思想方法，是中档题．
练习册系列答案
相关题目
在△ABC中，三边a，b，c所对的角分别为A，B，C，若a2-b2=
bc，sinC=2
sinB，则角A=（ ）
| 3 |
| 3 |
| A、30° | B、45° |
| C、150° | D、135° |
设|
|=2，|
|=3，∠BAC=60°，
=2
，
=x
+（1+x）
，x∈[0，1]，则
在
上的投影的取值范围是（ ）
| AB |
| AC |
| CD |
| BC |
| AE |
| AD |
| AB |
| AE |
| AC |
| A、[0，1] |
| B、[0，7] |
| C、[1，9] |
| D、[9，21] |
若直线2ax+by-2=0（a，b∈R+）平分圆x2+y2-2x-4y-6=0，则
+
的最小值是（ ）
| 2 |
| a |
| 1 |
| b |
| A、1 | ||
| B、5 | ||
C、4
| ||
D、3+2
|
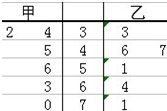近年来，我国许多地方出现雾霾天气，影响了人们的出行、工作与健康．其形成与PM2.5有关．PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．PM2.5日均值越小，空气质量越好．为加强生态文明建设，我国国家环保部于2012年2月29日，发布了《环境空气质量标准》见表：