题目内容

已知△ABC中，∠A，∠B，∠C的对边分别为a，b，c，若a=1且cosA=
4
5
，则△ABC的外接圆的直径等于（　　）
A、
4
5
B、
5
4
C、
3
5
D、
5
3
考点：正弦定理
专题：三角函数的求值
分析：由cosA的值，利用同角三角函数间的基本关系求出sinA的值，再由a的值，利用正弦定理即可求出△ABC的外接圆的直径．
解答： 解：∵A为三角形的内角，cosA=
4
5
，
∴sinA=
1-cos2A
=
3
5
，
∵a=1，
∴由正弦定理得：
a
sinA
=2R，R为△外接圆半径，
则△ABC的外接圆的直径2R=
1
3
5
=
5
3
．
故选：D．
点评：此题考查了正弦定理，以及同角三角函数间的基本关系，熟练掌握正弦定理是解本题的关键．
练习册系列答案
相关题目
过双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的左焦点F（-c，0）（c＞0），作圆x2+y2=
a2
4
的切线，切点为E，延长FE交双曲线右支于点P，若
OP
=2
OE
-
OF
，则双曲线的离心率为（　　）
A、
10
B、
10
5
C、
10
2
D、
2
log212-log23=（　　）
A、-2
B、0
C、
1
2
D、2
若
x≤2
y≤2
x+y≥3
，则目标函数z=
x+2y
x
的取值范围是（　　）
A、[2，5]
B、[1，5]
C、[
1
2
，2]
D、[2，6]
若直线2ax+by-2=0（a，b∈R+）平分圆x2+y2-2x-4y-6=0，则
2
a
+
1
b
的最小值是（　　）
A、1
B、5
C、4
2
D、3+2
2
已知函数f（x）=ax3+bx2在点（3，f（3））处的切线方程为12x+2y-27=0．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）若方程f(x)=-
1
2
x2+m有三个不同的解，求实数m的取值范围；
（Ⅲ）若不等式f(x)-
3
2
x2+(k+1)x≥0(k∈R)对于x∈（-∞，0）恒成立，求实数k的取值范围．
已知函数f（x）=
1
2
ax2-（2a+1）x+2lnx（a＞0）．
（Ⅰ）若a=
1
3
，求f（x）在[1，3]上的最大值；
（Ⅱ）若a≠
1
2
，求函数f（x）的单调区间；
（Ⅲ）当
1
2
＜a＜1时，判断函数f（x）在区间[1，2]上有无零点？写出推理过程．
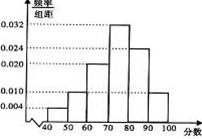某校高三年级发展均衡，各班均有学生50人，全校共有20个平行班级．随机选择一个班，将他们的期中数学考试成绩分成六段：[40，50），[50，60），…，[90，100]，得到如图所示频率分布直方图．
（1）请估计该校这20个班级中成绩不低于60分的人数；
（2）为了帮助学生提高数学成绩，该班班主任决定成立“二帮一”小组：对成绩在[40，50）内的每位同学，从成绩在[90，100]中选两位同学对其数学学习提供帮助，各组成员没有重复．已知甲成绩为42分，乙成绩为95分，求甲、乙恰好被安排在同一小组的概率．
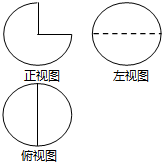一个几何体的三视图如图所示，其中俯视图与左视图均为半径是2的圆，则这个几何体的表面积是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网