题目内容
已知数列{an}的前n项和为Sn,对一切正整数n,点Pn(n,Sn)都在函数f(x)=x2+2x的图象上.
(1)求a1,a2;
(2)求数列{an}的通项公式;
(3)若bn=
,求证数列{bn}的前n项和Tn<
.
(1)求a1,a2;
(2)求数列{an}的通项公式;
(3)若bn=
| 1 |
| anan+1an+2 |
| 1 |
| 60 |
考点:数列与不等式的综合,数列的求和
专题:点列、递归数列与数学归纳法
分析:(1)把点Pn(n,Sn)代入函数f(x)=x2+2x,得到数列{an}的前n项和,分别取n=1,2求得a1,a2;
(2)直接由an=Sn-Sn-1(n≥2)求出数列通项,验证a1后得答案;
(3)把(2)中求得的数列的通项公式代入bn=
,利用裂项相消法求和后证明不等式Tn<
.
(2)直接由an=Sn-Sn-1(n≥2)求出数列通项,验证a1后得答案;
(3)把(2)中求得的数列的通项公式代入bn=
| 1 |
| anan+1an+2 |
| 1 |
| 60 |
解答:
(1)解:∵点Pn(n,Sn)都在函数f(x)=x2+2x的图象上,
∴Sn=n2+2n(n∈N*),
∴a1=S1=3,
又a1+a2=S2=22+2×2=8,
∴a2=5;
(2)解:由(1)知,Sn=n2+2n(n∈N*),
当n≥2时,an=Sn-Sn-1=2n+1.
由(1)知,a1=3=2×1+1满足上式,
∴数列{an}的通项公式为an=2n+1;
(3)证明:由(2)得,
bn=
=
[
-
]
∴Tn=b1+b2+…+bn
=
[
-
+
-
+…+
-
]
=
[
-
]=
-
<
.
∴Sn=n2+2n(n∈N*),
∴a1=S1=3,
又a1+a2=S2=22+2×2=8,
∴a2=5;
(2)解:由(1)知,Sn=n2+2n(n∈N*),
当n≥2时,an=Sn-Sn-1=2n+1.
由(1)知,a1=3=2×1+1满足上式,
∴数列{an}的通项公式为an=2n+1;
(3)证明:由(2)得,
bn=
| 1 |
| (2n+1)(2n+3)(2n+5) |
| 1 |
| 4 |
| 1 |
| (2n+1)(2n+3) |
| 1 |
| (2n+3)(2n+5) |
∴Tn=b1+b2+…+bn
=
| 1 |
| 4 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 5×7 |
| 1 |
| 7×9 |
| 1 |
| (2n+1)(2n+3) |
| 1 |
| (2n+3)(2n+5) |
=
| 1 |
| 4 |
| 1 |
| 3×5 |
| 1 |
| (2n+3)(2n+5) |
| 1 |
| 60 |
| 1 |
| 4(2n+3)(2n+5) |
| 1 |
| 60 |
点评:本题是数列与不等式的综合题,考查了数列的函数特性,训练了利用数列的前n项和求通项公式,考查了利用裂项相消法求数列的和,体现了放缩法证明不等式的解题思想,是中高档题.

练习册系列答案
相关题目
下列各组命题:
(1)p:a+b=2,q:直线x+y=0与圆(x-a)2+(y-b)2=2相切;
(2)p:|x|=x,q:x2+x≥0;
(3)设l,m均为直线,σ为平面,其中l?σ,m⊆σ,p:l∥σ,q:l∥m.
(4)p:数列log3n,log3(n+1),log3(n+3),(n∈N*)成等差数列;q:数列(
)n,
,3n(n∈N*)成等比数列.
其中,p是q的充分不必要条件的是( )
(1)p:a+b=2,q:直线x+y=0与圆(x-a)2+(y-b)2=2相切;
(2)p:|x|=x,q:x2+x≥0;
(3)设l,m均为直线,σ为平面,其中l?σ,m⊆σ,p:l∥σ,q:l∥m.
(4)p:数列log3n,log3(n+1),log3(n+3),(n∈N*)成等差数列;q:数列(
| 1 |
| 3 |
| 3 |
| 3n |
其中,p是q的充分不必要条件的是( )
| A、(1)(2) |
| B、(1)(4) |
| C、(1)(3) |
| D、(2)(3)(4) |
若函数f(x)=(x+1)(x-a)是偶函数,则实数a的值为( )
| A、1 | B、0 | C、-1 | D、±1 |
 如图,向量
如图,向量| OZ |
| 4 |
| z |
| A、1+3i | B、-3+i |
| C、3-i | D、3+i |
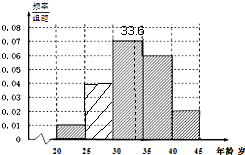 某市要对两千多名出租车司机的年龄进行调查,现从的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是( )
某市要对两千多名出租车司机的年龄进行调查,现从的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是( )| A、31.6岁 |
| B、32.6岁 |
| C、33.6岁 |
| D、36.6岁 |