题目内容
如图是某市2月1日至14日的空气质量指数趋势图,空气质量指数(AQI)小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择2月1日至2月12日中的某一天到达该市,并停留3天.
(1)求此人到达当日空气质量优良的概率;
(2)求此人停留期间至多有1天空气重度污染的概率.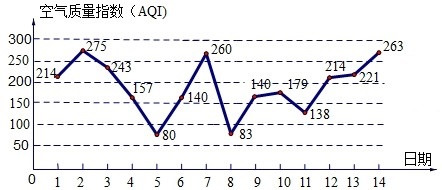
(1)求此人到达当日空气质量优良的概率;
(2)求此人停留期间至多有1天空气重度污染的概率.

考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)由图查出13天内空气质量指数小于100的天数,直接利用古典概型概率计算公式得到答案;
(2)用列举法写出此人在该市停留两天的空气质量指数的所有情况,查出仅有一天是重度污染的情况,然后直接利用古典概型概率计算公式得到答案.
(2)用列举法写出此人在该市停留两天的空气质量指数的所有情况,查出仅有一天是重度污染的情况,然后直接利用古典概型概率计算公式得到答案.
解答:
解:(1)在2月1日至2月12日这12天中,只有5日、8日共2天的空气质量优良,
∴此人到达当日空气质量优良的概率P=
=
.
(2)根据题意,事件“此人在该市停留期间至多有1天空气重度污染”,
即“此人到达该市停留期间0天空气重度污染或仅有1天空气重度污染”.
“此人在该市停留期间0天空气重度污染”等价于“此人到达该市的日期是4日或8日或9日”.
其概率为
=
,
“此人在该市停留期间仅有1天空气重度污染”等价于“此人到达该市的日期是3日或5日或6日或7日或10日”.
其概率为
,
∴此人停留期间至多有1天空气重度污染的概率为.P=
+
=
.
∴此人到达当日空气质量优良的概率P=
| 2 |
| 12 |
| 1 |
| 6 |
(2)根据题意,事件“此人在该市停留期间至多有1天空气重度污染”,
即“此人到达该市停留期间0天空气重度污染或仅有1天空气重度污染”.
“此人在该市停留期间0天空气重度污染”等价于“此人到达该市的日期是4日或8日或9日”.
其概率为
| 3 |
| 12 |
| 1 |
| 4 |
“此人在该市停留期间仅有1天空气重度污染”等价于“此人到达该市的日期是3日或5日或6日或7日或10日”.
其概率为
| 5 |
| 12 |
∴此人停留期间至多有1天空气重度污染的概率为.P=
| 1 |
| 4 |
| 5 |
| 12 |
| 2 |
| 3 |
点评:本题考查了古典概型及其概率计算公式,训练了学生的读图能力,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知点A(2,1)、B(1,3),直线ax-by+1=0(a,b∈R+)与线段AB相交,则(a-1)2+b2的最小值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
sin2013°∈( )
A、(-
| ||||||||
B、(-
| ||||||||
C、(
| ||||||||
D、(
|
设0<a<b,且f(x)=
,则下列大小关系式成立的是( )
1+
| ||
| x |
A、f (a)<f (
| ||||
B、f (
| ||||
C、f (
| ||||
D、f (b)<f (
|

 一个空间几何体的三视图如图所示,其正视图、侧视图、俯视图均为等腰直角三角形,且直角边长都为1,则这个几何体的体积是
一个空间几何体的三视图如图所示,其正视图、侧视图、俯视图均为等腰直角三角形,且直角边长都为1,则这个几何体的体积是