设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:
①有12个顶点;②有24条棱;③有12个面;④表面积为3a2;⑤体积为
a3.
其中正确的结论是( )
①有12个顶点;②有24条棱;③有12个面;④表面积为3a2;⑤体积为
| 5 |
| 6 |
其中正确的结论是( )
| A、①③④ | B、①②⑤ |
| C、②③⑤ | D、②④⑤ |
已知符号函数sgnx=
,则不等式(x2-2)•sgnx>1的解集是( )
|
A、(-1,1)∪(
| ||||
B、(-1,0)∪(
| ||||
C、(-∞,
| ||||
D、(-∞,-
|
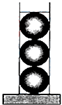 圆柱形容器内盛有高度为4cm的水,若放入三个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图),则球的表面积是( )
圆柱形容器内盛有高度为4cm的水,若放入三个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图),则球的表面积是( )| A、2π | B、4π | C、8π | D、16π |

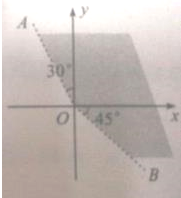 如图,终边落在OA位置的角α的集合是
如图,终边落在OA位置的角α的集合是