题目内容
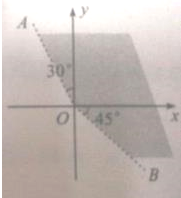 如图,终边落在OA位置的角α的集合是
如图,终边落在OA位置的角α的集合是考点:终边相同的角
专题:直线与圆
分析:利用终边相同的角的集合定理可得出分别与角120°,45°终边相同的角,即可终边落在阴影区域(包括边界)的角的集合.
解答:
解:分别与角120°,45°终边相同的角为120°+k•360°,45°+k•360°(k∈Z).
因此终边落在阴影区域(包括边界)的角的集合是{α|45°+k•360°≤α≤120°+k•360°,k∈Z}.
故答案为:{α|α=120°+k•360°,k∈z};{α|α=45°+k•360°,k∈z};{α|45°+k•360°≤α≤120°+k•360°,k∈Z}.
因此终边落在阴影区域(包括边界)的角的集合是{α|45°+k•360°≤α≤120°+k•360°,k∈Z}.
故答案为:{α|α=120°+k•360°,k∈z};{α|α=45°+k•360°,k∈z};{α|45°+k•360°≤α≤120°+k•360°,k∈Z}.
点评:本题考查终边相同的角的定义和表示方法,根据图形表示出满足条件的角的集合,注意要注明k∈z.

练习册系列答案
相关题目
已知R是实数集,集合P={x|y=ln(x2+2014x-2015)},Q={y|y=
},则(∁RP)∪Q( )
| -x2+2x+3 |
| A、(0,1] |
| B、[0,1] |
| C、(-2015,1] |
| D、[-2015,2] |
从0,1,2,3,4,5这六个数字中,任取两个不同数字相加,其和为偶数的不同取法的种数有( )
| A、30 | B、20 | C、10 | D、6 |

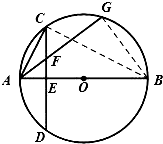 已知,AB为圆O的直径,CD为垂直AB的一条弦,垂足为E,弦AG交CD于F.
已知,AB为圆O的直径,CD为垂直AB的一条弦,垂足为E,弦AG交CD于F.