题目内容
已知集合A={x||x-1|+|x+1|≤3},集合B={x|x2-(2m+1)x+m2+m<0}若,A∩B≠∅,则实数m的取值范围为 .
考点:绝对值不等式的解法,一元二次不等式的解法
专题:不等式的解法及应用
分析:化简集合A,B,结合A∩B≠∅,得到端点的关系求m.
解答:
解:由已知A=[-
,
],B=(m,m+1),
如果A∩B=∅,则m>
或者m+1<-
,
所以要使A∩B≠∅,只要m∈(-
,
);
故答案为:(-
,
);
| 3 |
| 2 |
| 3 |
| 2 |
如果A∩B=∅,则m>
| 3 |
| 2 |
| 3 |
| 2 |
所以要使A∩B≠∅,只要m∈(-
| 5 |
| 2 |
| 3 |
| 2 |
故答案为:(-
| 5 |
| 2 |
| 3 |
| 2 |
点评:本题考查了绝对值不等式以及一元二次不等式的解法和集合的运算,注意问题的转化.

练习册系列答案
相关题目
设函数f(x)=(x2-8x+c1)(x2-8x+c2)(x2-8x+c3) (x2-8x+c4),集合M={x|f(x)=0}={x1,x2…,x7}⊆N+,设c1≥c2≥c3≥c4,则c1-c4( )
| A、9 | B、8 | C、7 | D、6 |
从0,1,2,3,4,5这六个数字中,任取两个不同数字相加,其和为偶数的不同取法的种数有( )
| A、30 | B、20 | C、10 | D、6 |
一个几何体的三视图如图所示(单位:m),则该几何体的体积为( )
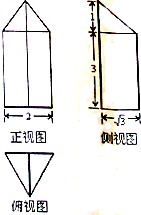

A、2
| ||||
B、4
| ||||
C、
| ||||
D、
|
球的半径为2,它的内接正方体的表面积为( )
| A、8 | B、16 | C、32 | D、64 |