题目内容
已知p:?x∈R,4x2+4(m-2)x+1≠0;q:?x1,x2∈(-∞,0)且x1≠x2,x2+mx+1=0
(1)写出¬p和¬q;
(2)若(¬p)或¬q为假命题,求m的取值范围.
(1)写出¬p和¬q;
(2)若(¬p)或¬q为假命题,求m的取值范围.
考点:复合命题的真假
专题:计算题,简易逻辑
分析:(1)利用命题的否定,可得¬p和¬q;
(2)先求出p为真命题且q也为真命题,m的取值范围,即可得出结论.
(2)先求出p为真命题且q也为真命题,m的取值范围,即可得出结论.
解答:
解:(1)∵p:?x∈R,4x2+4(m-2)x+1≠0;q:?x1,x2∈(-∞,0)且x1≠x2,x2+mx+1=0
∴¬p:?x∈R,4x2+4(m-2)x+1=0;q:?x1,x2∈(-∞,0)且x1≠x2,x2+mx+1≠0;
(2)若p为真,则△=16(m-2)2-16<0,解得1<m<3.
若q为真,则
,解得m>2.
∴p为真命题且q也为真命题即
∴m的取值范围是(2,3).
∴(¬p)或¬q为假命题,m的取值范围是(-∞,2)∪(3,+∞).
∴¬p:?x∈R,4x2+4(m-2)x+1=0;q:?x1,x2∈(-∞,0)且x1≠x2,x2+mx+1≠0;
(2)若p为真,则△=16(m-2)2-16<0,解得1<m<3.
若q为真,则
|
∴p为真命题且q也为真命题即
|
∴m的取值范围是(2,3).
∴(¬p)或¬q为假命题,m的取值范围是(-∞,2)∪(3,+∞).
点评:复合命题的真假判断是解决本题的突破口,充要条件是解决本题的出发点,本题设计新颖,难于理解.

练习册系列答案
相关题目
已知集合A={x|x<a},B={x|2<x<4},且A∪(∁RB)=R,则实数a的取值范围( )
| A、a≤4 | B、a<2 |
| C、a>4 | D、a≥4 |
盒中有4个相同的球,标号1,2,3,4.现从盒中随机摸一个,若摸出球上的数字是被摸球中最大的则留下,否则放回,则5次内(包括5次)把球摸完的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
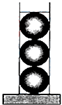 圆柱形容器内盛有高度为4cm的水,若放入三个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图),则球的表面积是( )
圆柱形容器内盛有高度为4cm的水,若放入三个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图),则球的表面积是( )| A、2π | B、4π | C、8π | D、16π |
空间4点A,B,C,D共面但不共线,下列结论中正确的是( )
| A、4点中必能找出其中3点共线 |
| B、4点中必能找出其中3点不共线 |
| C、AB,BC,CD,DA中必有两条平行 |
| D、AB与CD必相交 |
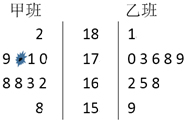 随机抽取某中学高三年级甲乙两班各10名同学,测量出他们的身高(单位:cm),获得身高数据的茎叶图如图.其中甲班有一个数据被污损.
随机抽取某中学高三年级甲乙两班各10名同学,测量出他们的身高(单位:cm),获得身高数据的茎叶图如图.其中甲班有一个数据被污损.