题目内容
在数学中,等与不等是相对的,例如“当a≤b且a≥b时,我们就可以得到a=b”.设二次函数f(x)=ax2+bx+c(a,b,c∈R),且满足f(-1)=0,对于任意实数x都有f(x)-x≥0,且当x∈(0,2)时,f(x)≤(
)2.
(Ⅰ)求f(1)的值;
(Ⅱ)求证:a>0,c>0;
(Ⅲ)当x∈[-1,1]时,函数g(x)=f(x)-mx(m∈R)是单调的,求实数m的取值范围.
| x+1 |
| 2 |
(Ⅰ)求f(1)的值;
(Ⅱ)求证:a>0,c>0;
(Ⅲ)当x∈[-1,1]时,函数g(x)=f(x)-mx(m∈R)是单调的,求实数m的取值范围.
考点:函数单调性的性质,基本不等式
专题:函数的性质及应用
分析:(I)由于对于任意实数x都有f(x)-x≥0,且当x∈(0,2)时,f(x)≤(
)2.可得f(1)≥1,f(1)≤(
)2=1.
(II)由
可得b=a+c=
.对于任意实数x都有f(x)-x≥0,可得ax2-
x+c≥0,
,即可得出;
(III)由于
=a+c≥2
≥2
=
,可得a=c=
.可得g(x)=f(x)-mx=
x2+(
-m)x+
,由于当x∈[-1,1]时,函数g(x)=f(x)-mx(m∈R)是单调的,再利用二次函数的单调性即可得出.
| x+1 |
| 2 |
| 1+1 |
| 2 |
(II)由
|
| 1 |
| 2 |
| 1 |
| 2 |
|
(III)由于
| 1 |
| 2 |
| ac |
|
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
解答:
(I)解:∵对于任意实数x都有f(x)-x≥0,且当x∈(0,2)时,f(x)≤(
)2.
∴f(1)≥1,f(1)≤(
)2=1.
∴f(1)=1.
(II)证明:由
可得
,∴b=a+c=
.
对于任意实数x都有f(x)-x≥0,即ax2+(b-1)x+c≥0,
∴ax2-
x+c≥0,∴
,
∴a>0,ac≥
,∴a>0,c>0.
(III)∵
=a+c≥2
≥2
=
,∴a=c=
.
∴f(x)=
x2+
x+
,
∴g(x)=f(x)-mx=
x2+(
-m)x+
,
∴g(x)=
[x2+(2-4m)x+1].
又∵当x∈[-1,1]时,函数g(x)=f(x)-mx(m∈R)是单调的,
∴|
|≥1,解得m≥1或m≤0.
| x+1 |
| 2 |
∴f(1)≥1,f(1)≤(
| 1+1 |
| 2 |
∴f(1)=1.
(II)证明:由
|
|
| 1 |
| 2 |
对于任意实数x都有f(x)-x≥0,即ax2+(b-1)x+c≥0,
∴ax2-
| 1 |
| 2 |
|
∴a>0,ac≥
| 1 |
| 16 |
(III)∵
| 1 |
| 2 |
| ac |
|
| 1 |
| 2 |
| 1 |
| 4 |
∴f(x)=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴g(x)=f(x)-mx=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
∴g(x)=
| 1 |
| 4 |
又∵当x∈[-1,1]时,函数g(x)=f(x)-mx(m∈R)是单调的,
∴|
| 2-4m |
| 2 |
点评:本题考查了二次函数的单调性、基本不等式的性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设 H1(X)=max{f(x),g(x)},max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值,记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
| A、a2-2a-16 |
| B、a2+2a-16 |
| C、16 |
| D、-16 |
已知集合A={x∈N|1<x<5},集合B={x∈N|2<x<6},则A∩B=( )
| A、{2,3} |
| B、{4,3} |
| C、{5,3} |
| D、{44,5} |
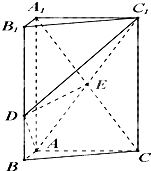 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=2,AC=6,点D在线段BB1上,且BD=
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=2,AC=6,点D在线段BB1上,且BD=