题目内容
一个几何体的三视图如图所示，则此几何体的体 积是 ．
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：根据几何体的三视图，知该几何体是圆柱与半球的组合体，结合题中数据求出它的体积．
解答：
解：根据几何体的三视图，得；
该几何体底部是半径为4、高为3的圆柱，
顶部是半径为4的半球；
它的体积是
V几何体=V圆柱+V半球=π•42•3+
•
•π•43=
π．
故答案为：
π．
该几何体底部是半径为4、高为3的圆柱，
顶部是半径为4的半球；
它的体积是
V几何体=V圆柱+V半球=π•42•3+
| 1 |
| 2 |
| 4 |
| 3 |
| 272 |
| 3 |
故答案为：
| 272 |
| 3 |
点评：本题考查了三视图的应用问题，也考查了求几何体的体积问题，是基础题．
练习册系列答案
相关题目
设集合A={1，3，a}，B={1，2}且A?B，则a的值为（ ）
| A、0 | B、1 | C、2 | D、3 |
已知符号函数sgnx=
，则不等式（x2-2）•sgnx＞1的解集是（ ）
|
A、(-1，1)∪(
| ||||
B、(-1，0)∪(
| ||||
C、(-∞，
| ||||
D、(-∞，-
|
二直线mx+3y+3=0，2x+（m-1）y+2=0平行，则实数m的值为（ ）
| A、3或-2 | B、-3或2 |
| C、3 | D、-2 |
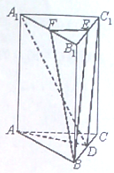如图，在三棱柱ABC-A1B1C1中，底面为正三角形，AA1⊥平面ABC，D，E，F分别为BC，B1C1，A1B1的中点．