题目内容
设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:
①有12个顶点;②有24条棱;③有12个面;④表面积为3a2;⑤体积为
a3.
其中正确的结论是( )
①有12个顶点;②有24条棱;③有12个面;④表面积为3a2;⑤体积为
| 5 |
| 6 |
其中正确的结论是( )
| A、①③④ | B、①②⑤ |
| C、②③⑤ | D、②④⑤ |
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:先根据题意画出图形,如图,原来的六个面仍然在,但是却变成了一个小正方形,再添了八个顶点各对应的一个三角形的面,计算或数一数它的顶点数目、棱数及面数,可判断①、②、③;
再结合割补法求出它的表面积及体积,可判断④与⑤.
再结合割补法求出它的表面积及体积,可判断④与⑤.
解答:
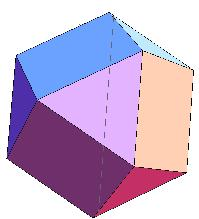 解:如图,
解:如图,
对于①,由于所有的顶点都出现在原来正方体的棱的中点位置,原来的棱的数目是12,所以现在的顶点的数目是12,故①正确;
对于②,每个正方形4条边,每个三角形3条边,4×6+3×8=48,考虑到每条边对应两个面,所以实际只有
×48=24(从图片上可以看出每个顶点对应4条棱,每条棱很明显对应两个顶点,所以棱数为
×48=24个),故②正确;
对于③,原来的六个面仍在,却是变成了一个小正方形,且添了八个顶点各对应的一个三角形的面,所以总计6+8=14个面,
故③错;
对于④,三角形和四边形的边长都是
a,所以正方形总面积为6×
a2=3a2,三角形总面积为8×
×
a2sin60°=
a2,
表面积(3+
)a2,故④错;
对于⑤,体积为原正方形体积减去8个三棱锥体积,每个三棱锥体积为8×
×(
)3=
a3,剩余总体积为a3-
a3=
a3.
故⑤正确.
故选:B.
 解:如图,
解:如图,对于①,由于所有的顶点都出现在原来正方体的棱的中点位置,原来的棱的数目是12,所以现在的顶点的数目是12,故①正确;
对于②,每个正方形4条边,每个三角形3条边,4×6+3×8=48,考虑到每条边对应两个面,所以实际只有
| 1 |
| 2 |
| 1 |
| 2 |
对于③,原来的六个面仍在,却是变成了一个小正方形,且添了八个顶点各对应的一个三角形的面,所以总计6+8=14个面,
故③错;
对于④,三角形和四边形的边长都是
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
表面积(3+
| 3 |
对于⑤,体积为原正方形体积减去8个三棱锥体积,每个三棱锥体积为8×
| 1 |
| 6 |
| a |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
| 5 |
| 6 |
故⑤正确.
故选:B.
点评:本题主要考查棱柱的结构特征,多面体的表面积与体积等基础知识,考查化归思想与空间想象能力、运算求解能力,属于难题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
在正方体ABCD-A1B1C1D1中,A1D与BC1所成的角为( )
| A、30° | B、45° |
| C、60° | D、90° |
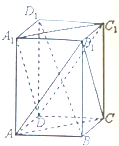 如图,在长方体ABCD-A1B1C1D1中,BB1=BC.
如图,在长方体ABCD-A1B1C1D1中,BB1=BC.