题目内容
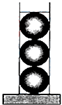圆柱形容器内盛有高度为4cm的水，若放入三个相同的铁球（球的半径与圆柱的底面半径相同）后，水恰好淹没最上面的球（如图），则球的表面积是（ ）| A、2π | B、4π | C、8π | D、16π |
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：设出球的半径，三个球的体积和水的体积之和，等于柱体的体积，求解即可．
解答：
解：设球半径为r，则由3V球+V水=V柱可得3×
πr3+πr2×4=πr2×6r，解得r=2．
∴球的表面积是4π×4=16π．
故选：D．．
| 4 |
| 3 |
∴球的表面积是4π×4=16π．
故选：D．．
点评：本题考查几何体的体积，考查球的表面积，考查学生空间想象能力，是基础题．
练习册系列答案
相关题目
中心城区现有绿化面积为1000hm2，计划每年增长4%，经过x（x∈N*）年，绿化面积为y hm2，则x，y间的函数关系式为（ ）
| A、y=1000（1+4%）x（x∈N*） |
| B、y=（1000×4%）x（x∈N*） |
| C、y=1000（1-4%）x （x∈N*） |
| D、y=1000（4%）x（x∈N*） |
设集合S={y|y=（
）x-1，x∈R}，T={y|y=log2（x+2）}，S∪T=（ ）
| 1 |
| 2 |
| A、S | B、T |
| C、R | D、[-1，+∞） |
将棱长为1的正方体木块切削成一个体积最大的球，则该球的体积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|