已知圆(x-3)2+(y-4)2=4和直线y=x相交于P,Q两点则|OP|•|OQ|的值是( )
A、
| ||
| B、2 | ||
| C、4 | ||
| D、21 |
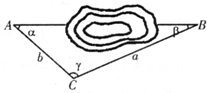 如图,为了测量隧道两口之间AB的长度,对给出的四组数据,求解计算时,较为简便易行的一组是( )
如图,为了测量隧道两口之间AB的长度,对给出的四组数据,求解计算时,较为简便易行的一组是( )| A、a,b,γ |
| B、a,b,α |
| C、a,b,β |
| D、α,β,a |
A、
| ||
| B、2 | ||
| C、4 | ||
| D、21 |
 如图,为了测量隧道两口之间AB的长度,对给出的四组数据,求解计算时,较为简便易行的一组是( )
如图,为了测量隧道两口之间AB的长度,对给出的四组数据,求解计算时,较为简便易行的一组是( )| A、a,b,γ |
| B、a,b,α |
| C、a,b,β |
| D、α,β,a |