题目内容
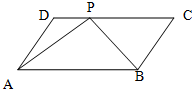 如图,在四边形ABCD中,
如图,在四边形ABCD中,| AB |
| DC |
| AB |
| AD |
| AB |
| AD |
| 11 |
| 20 |
| CP |
| PD |
| AP |
| BP |
| A、2 | B、4 | C、6 | D、10 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由
=3
,可得
=
+
,
=
-
,进而由AB=8,AD=5,cosθ=
,利用向量数量积运算进而可得答案.
| CP |
| PD |
| AP |
| AD |
| 1 |
| 4 |
| AB |
| BP |
| AD |
| 3 |
| 4 |
| AB |
| 11 |
| 20 |
解答:
解:解:∵
=3
,∴
=
+
,
=
-
,
又∵AB=8,AD=5,
∴
•
=(
+
)•(
-
)=
2-
•
-
2=25-
×8×5cosθ-
×82=25-
×8×5×
-12=2.
故选A.
| CP |
| PD |
| AP |
| AD |
| 1 |
| 4 |
| AB |
| BP |
| AD |
| 3 |
| 4 |
| AB |
又∵AB=8,AD=5,
∴
| AP |
| BP |
| AD |
| 1 |
| 4 |
| AB |
| AD |
| 3 |
| 4 |
| AB |
| AD |
| 1 |
| 2 |
| AD |
| AB |
| 3 |
| 16 |
| AB |
| 1 |
| 2 |
| 3 |
| 16 |
| 1 |
| 2 |
| 11 |
| 20 |
故选A.
点评:本题考查的知识点是向量在几何中的应用,平面向量数量积的运算,其中根据
=3
,可得
=
+
,
=
-
,是解答的关键,属于中档题.
| CP |
| PD |
| AP |
| AD |
| 1 |
| 4 |
| AB |
| BP |
| AD |
| 3 |
| 4 |
| AB |

练习册系列答案
相关题目
将直线2x-y+λ=0沿x轴向右平移1个单位,所得直线与圆x2+y2+2x-4y=0相切,则实数λ的值为( )
| A、-3或7 | B、-2或8 |
| C、0或10 | D、1或11 |
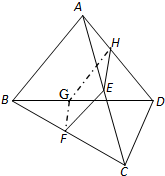 如图,在四面体ABCD中,平行于AB,CD的平面β截四面体所得截面为EFGH.
如图,在四面体ABCD中,平行于AB,CD的平面β截四面体所得截面为EFGH.