题目内容
过双曲线
-
=1(b>0)左焦点F1的直线l与双曲线左支交于A,B两点,若|AF2|+|BF2|(F2是双曲线的右焦点)的最小值为14,则b的值是 ( )
| x2 |
| 9 |
| y2 |
| b2 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据双曲线的标准方程可得:a=3,再由双曲线的定义可得:|AF2|-|AF1|=2a=6,|BF2|-|BF1|=2a=6,所以得到|AF2|+|BF2|-(|AF1|+|BF1|)=12,再根据A、B两点的位置特征得到答案.
解答:
解:根据双曲线的标准方程
-
=1(b>0),得:a=3,
由双曲线的定义可得:|AF2|-|AF1|=2a=6…①,
|BF2|-|BF1|=2a=6…②,
①+②可得:|AF2|+|BF2|-(|AF1|+|BF1|)=12,
∵过双曲线的左焦点F1的直线交双曲线的左支于A,B两点,
∴|AF1|+|BF1|=|AB|,当|AB|是双曲线的通径时|AB|最小.
∴|AF2|+|BF2|-(|AF1|+|BF1|)=|AF2|+|BF2|-|AB|=12.
∴|BF2|+|AF2|=|AB|+12≥
+12=14,
∴b=
.
故选:C.
| x2 |
| 9 |
| y2 |
| b2 |
由双曲线的定义可得:|AF2|-|AF1|=2a=6…①,
|BF2|-|BF1|=2a=6…②,
①+②可得:|AF2|+|BF2|-(|AF1|+|BF1|)=12,
∵过双曲线的左焦点F1的直线交双曲线的左支于A,B两点,
∴|AF1|+|BF1|=|AB|,当|AB|是双曲线的通径时|AB|最小.
∴|AF2|+|BF2|-(|AF1|+|BF1|)=|AF2|+|BF2|-|AB|=12.
∴|BF2|+|AF2|=|AB|+12≥
| 2b2 |
| 3 |
∴b=
| 3 |
故选:C.
点评:本题考查两条线段和的最小值的求法,是中档题,解题时要注意双曲线的简单性质的合理运用.

练习册系列答案
相关题目
若m.n是两条不同的直线,α、β是两个不同的平面,则下列命题不正确的是( )
| A、若α∥β,m⊥α,则m⊥β |
| B、若α∩β=m,n与α、β所成的角相等,则m⊥n |
| C、若m∥α,m⊥β,则α⊥β |
| D、若m∥n,m⊥α,则n⊥α |
 如图,正方形ABCD中,E,F分别是AB,BC的中点,O是EF的中点,现在沿DE,DF及EF把这个正方形折成一个四面体,使A,B,C三点重合,重合后的点记为G,则在四面体D-EFG中必有( )
如图,正方形ABCD中,E,F分别是AB,BC的中点,O是EF的中点,现在沿DE,DF及EF把这个正方形折成一个四面体,使A,B,C三点重合,重合后的点记为G,则在四面体D-EFG中必有( )| A、GF⊥△DEF所在平面 |
| B、DO⊥△EFG所在平面 |
| C、DG⊥△EFG所在平面 |
| D、GO⊥△EFG所在平面 |
如图是计算t=12×22×…×i2的程序,程序中循环体执行的次数为( )


| A、3 | B、4 | C、5 | D、6 |
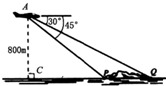 某次飞行表演中,一架直升从空中A处测出前下方海岛两侧海岸P、Q处的俯角分别是45°和30°(如右图所示,A、P、Q在同一平面内).
某次飞行表演中,一架直升从空中A处测出前下方海岛两侧海岸P、Q处的俯角分别是45°和30°(如右图所示,A、P、Q在同一平面内).