题目内容
已知AB为过双曲线C的一个焦点F且垂直于实轴的弦,且|AB|为双曲线C的实轴长的2倍,则双曲线C的离心率为 .
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设双曲线C:
-
=1,焦点F(c,0),由题设知
=2a=2a,由此能够推导出C的离心率.
| x2 |
| a2 |
| y2 |
| b2 |
| b2 |
| a |
解答:
 解:设双曲线C:
解:设双曲线C:
-
=1,焦点F(c,0),
-
=1,焦点F(c,0),对称轴y=0,
由题设知
=2a=
b2=2a2,
c2-a2=2a2,
c2=3a2,
∴e=
=
.
故答案为:
.
 解:设双曲线C:
解:设双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
由题设知
| b2 |
| a |
b2=2a2,
c2-a2=2a2,
c2=3a2,
∴e=
| c |
| a |
| 3 |
故答案为:
| 3 |
点评:本题考查双曲线的性质和应用,解题时要注意公式的灵活运用.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
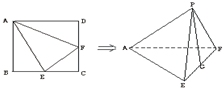 已知正方形ABCD的边长为2,点E、F分别为边BC,CD的中点,沿AE、EF、AF折叠成一个三棱锥P-AEF(使B,C,D重合于点P),则三棱锥P-AEF的外接球的表面积为( )
已知正方形ABCD的边长为2,点E、F分别为边BC,CD的中点,沿AE、EF、AF折叠成一个三棱锥P-AEF(使B,C,D重合于点P),则三棱锥P-AEF的外接球的表面积为( )A、8
| ||
| B、36π | ||
| C、12π | ||
| D、6π |
设x,y满足的条件
若z=x+3y+m的最小值为4,则m=( )
|
| A、1 | B、2 | C、3 | D、4 |